Journal of Financial Planning: November 2016
Stephen J. Huxley, Ph.D., is a tenured professor of business analytics at the University of San Francisco where he has taught in the School of Management since 1973. He won the Franz Edelman Prize for Outstanding Research in Management Science in 1988 and is co-author of Asset Dedication. He is co-founder and chief investment strategist for Asset Dedication LLC.
J. Brent Burns is co-founder and president of Asset Dedication LLC and co-author of Asset Dedication. He is an adjunct professor at the University of San Francisco School of Management where he teaches business analytics and personal financial planning.
Jeremy Fletcher, CFA, is director of investments and portfolio risk management of Asset Dedication LLC. Previously, he was a portfolio manager responsible for more than $2 billion in fixed income assets at American Century Investments, including directing the firm-wide strategy for inflation-linked products and managing the firm’s series of zero-coupon funds.
Executive Summary
- Equity yield curves establish the importance of time segmentation for equity returns as well as bonds: time is a factor in returns every bit as much as style and size. Optimal allocations thus depend on how time is segmented for planning purposes.
- This analysis used Center for Research in Security Prices data back to 1928 for returns on U.S. equity asset classes based on style and size, plus commodities and real estate. It compared performance of three passive investment strategies optimized with mathematical programming over one- to 40-year holding periods.
- Results showed that all three strategies produced equity yield curves. Strategy A adjusted for risk by focusing on minimum return. Strategy B adjusted for risk by focusing on volatility, and Strategy C made no adjustments for risk.
- Strategy A led to positive minimum returns within six years, while B and C required 15 years. Strategy C led to the highest average returns but the worst downside. Strategy B had average returns higher than Strategy A and lower than C, and worse minimum returns than A but better than C.
Most financial planners are familiar with bond yield curves. For each maturity date, a bond’s yield to maturity (YTM), by definition, is an approximation that is considered the best indicator of the worst-case return if the bond is held to maturity.1 For bonds, these worst-case returns are nearly always positive and upwardly sloping. As the time horizon increases, typically so does YTM, though its rise starts to taper off the longer the horizon. The U.S. Treasury publishes them online daily at treasury.gov/resource-center/data-chart-center/interest-rates, and videos are available online that animate historical bond yield curves.2
Equity yield curves also exist. That is, the return on equities is also based on the length of time equities are held. But it is not the average return where time matters most.3 Rather, it is the minimum return for a given time horizon (“time horizon” and “holding period” are used interchangeably here). These minimum return curves are not exactly the same as bond yield curves. They are not based on fixed cash flows of coupons and redemptions; they simply track the worst-case scenario in history for various asset classes over holding periods ranging from one to 40 years. But when plotted against time, they closely resemble bond yield curves.
Time is a critical component in personal financial planning. Most financial plans look ahead to identify and develop strategies to meet financial goals over an investor’s lifetime. Lifetimes can be broken up into a sequence of years, each with its own specific spending need. Some spending needs are rather easy to predict, such as budgeted living expenses (food, clothing, and shelter), while others are not (emergencies, weddings, layoffs, etc.). The point is that good planning typically requires segmenting life on a year-by-year basis and taking appropriate actions to fund each year.
At a very granular level, bonds themselves present the case for time segmentation. For example, according to dedicated portfolio theory (Leibowitz 1986a; Leibowitz 1986b; Sharpe, Alexander, and Baily 2001), a retired investor who, through the financial planning process, has identified a target spending need in seven years should fund that spending need with a bond that matures in seven years and delivers the precise amount of projected cash need. The eighth-year spending need should be funded with the eight-year bond and so on. Institutions, like pension funds, call this “liability-driven investing.” Liability-driven investing seeks to align the timing of a spending need with an asset that can predictably deliver the necessary cash flows when needed—no more, no less. A series of bonds with maturities ranging from one to 10 years can therefore fund 10 years of retirement spending with certainty. Each year can be segmented into its own silo where a bond is dedicated to funding that year’s need.
Where do equities fit into this picture? Consider a retired investor with 30 years of retirement income to fund. That means 30 time segments exist. Unfortunately, given the current low interest rates, most retired investors cannot fund 30 years of retirement spending with 30 years of bonds (government, corporate, muni, or otherwise). Investors who have a withdrawal rate above the yield curve, which is the case for most retirees, cannot purchase an all-bond portfolio that will last the entire horizon to meet the target spending needs. The cash flows would simply not be enough and the portfolio would fail. Therefore, many investors must take on equity exposure to improve the probability of achieving a portfolio sufficient to cover lifetime financial goals. As with bonds, it makes sense that the equity portion of the investor’s portfolio should also align with the investor’s spending needs, albeit the longer dated spending needs.
In this paper, three equity strategies were examined to determine which would be more consistent with a time segmentation approach and better support the goals of a financial plan and perhaps work better from a behavioral perspective as well. The three equity strategies were tested over 40 different holding periods (one-year, two-year, etc., up to 40-year holding periods) to estimate the effect of the length of the holding period on performance.
Time Segmentation in Equity Investing
Time segmentation for equities has not been broadly studied. This lack of research is partly due to a crucial difference between institutional investors and individual investors. As Harry Mark-
owitz famously noted in his Nobel Laureate lecture, modern portfolio theory (MPT) was developed primarily for “large (usually institutional) investors.”4 But most individuals are not like institutions. Clearly, they have less money, but they also have finite lifetimes. This makes time horizons inherent to the personal financial planning process, and building equity portfolios that best match an individual investor’s time horizon becomes critical (Blanchett, Finke, and Pfau 2014).
From a practical standpoint, part of the lack of research regarding equity yield curves may be due simply to the fact that equity yield curves have seldom, if ever, been seen. Unlike the ubiquitous bond yield curve, they simply do not show up in academic journals, trade publications, or anywhere else. Without visuals, they remain an abstract concept seldom considered in any direct way. Equity yield curves, and the importance to time segmentation that they imply, only become obvious when one plots minimum returns (the worst-case scenarios) that a portfolio might earn over successively longer time horizons.
In the context of a financial plan, periods of poor equity returns put pressure on an investor’s portfolio. Markets that produce returns above the target returns for the plan, or even average returns, usually work out fine for the investor. It is bad markets that can cause trouble, especially if they happen early in retirement.
Plotting minimum returns means plotting the worst-case scenario over all one-year periods, two-year periods, etc., up to 40-year periods. Minimum returns may actually be a better way to express the risks that commonly worry investors most: what would happen in the nastiest situation?
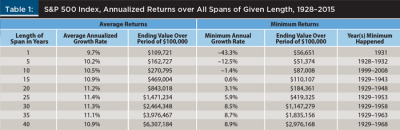
Figure 1 shows the minimum annualized total returns for the S&P 500 over holding periods of one, five, 10, 20, 30, and 40 years, based on a historical audit from 1928 to 2015 using data from the Center for Research in Security Prices (CRSP), available at www.crsp.com.

Figure 1 is based on Table 1, which shows average and minimum returns and when they occurred. Not surprisingly, the worst 10-year span was 1999 to 2008 when the index lost 1.4 percent per year. Not shown is the second-worst 10-year span, losing 0.95 percent per year from 2000 to 2009, nor the third-worst losing 0.89 percent per year from 1929 to 1938. Also, it is not surprising that the Great Depression was responsible for all of the other worst-case scenarios.
Three Strategies Based on Investment Goals
What strategy will achieve an optimal portfolio? Unfortunately, a unifying, all-encompassing strategy does not, and cannot, exist because the “optimal” strategy depends on the goal for the portfolio. Trade-offs, like the familiar volatility/return trade-off, must be made.
The three strategies listed below are designed to optimize different goals for a portfolio:
- Strategy A: minimize the worst-case scenario
- Strategy B: maximize the Sharpe ratio
- Strategy C: maximize expected returns
Strategy A: minimize the worst-case scenario (the “minimax” principle). Strategy A was the most conservative from a financial planning perspective. It considered “risk” to be the worst return that the portfolio has ever earned for a given horizon, not the volatility of its returns. Strategy A sought the allocation that minimized the worst-case returns for each time horizon. If the portfolio return was actually negative, it would seek to make the loss as small as possible. In other words, Strategy A sought to minimize the maximum loss (worst case). Hence the name “minimax.”
Planners familiar with Bengen’s “SAFEMAX” concept are well aware of this idea. SAFEMAX, otherwise known as “the 4 percent rule,” indicated the highest initial withdrawal (plus the prior year’s inflation) that a retiree could pull from a 50/50 stock/bond portfolio that would be sustainable over a 30-year span (Bengen 1994). That is, even in the worst 30-year period, the portfolio would not have failed until after 30 years had passed.
The minimax principle is rooted in the work of John von Neumann, whom many believe was the greatest mathematician of the 20th century (Halmos 1973; Macrae 1992). He was one of the founding fathers of the field of decision analysis and game theory. A contemporary of Albert Einstein, he is credited with discovering the minimax principle. The idea in decision theory is that, when deciding among several alternative courses of action, some of which could result in a loss, it is optimal to make the best of a bad situation by choosing the action that will lose the least if the worst-case scenario does, in fact, happen. Abraham Wald also contributed to this theory (Wald 1945). Because it is poor market returns that put stress on a financial plan, the minimax solution in portfolio theory is congruent with the goal of most conservative investors.
The differences between the average and worst performance can be dramatic. For example, Table 1 reveals that over the average 10-year period, the S&P 500 gained 10.5 percent per year ($100,000 would have grown to $270,795). But over its worst span, 1999 to 2008, it lost 1.4 percent per year ending at $87,008. After inflation, it would be even lower in real terms. The differences between average and minimum returns were larger for midcap (12.0 percent and –2.1 percent, respectively) and small-cap investments (12.9 percent and –2.6 percent). Clearly, investors expecting “average” results would be very concerned if they happen to invest during the worst bad period or even a poor one.
This intuitive insight is backed up by the behavioral economics concept known as prospect theory (Kahneman and Tversky 1979). According to this theory, most investors, especially conservative investors, dislike losses more than they favor gains, and would likely be quite concerned about the worst-case scenario. It is therefore reasonable that they choose an investment strategy that seeks to minimize the damage that a worst loss could create. Among the first to apply the minimax principle to investing was Martin Young, who examined it from the standpoint of management science and utility theory (Young 1998).
Strategy B: maximize the Sharpe ratio. The second strategy sought to maximize the “efficiency” of the portfolio according to modern portfolio theory, utilizing a mean-variance optimization routine that sought to maximize the Sharpe ratio—the most common strategy used in the industry. The Sharpe ratio subtracts the return of a risk-free asset from the actual return each year (or quarter or month) of some asset and divides the result by the standard deviation, all over the same time period. To a statistician, the Sharpe ratio is the inverse of the “coefficient of variation” after making adjustments for the risk-free asset.

A portfolio whose allocations among the available asset classes have the highest Sharpe ratio is considered to be an “efficient” portfolio because it is delivering the highest possible expected return per unit of volatility. The risk-free return is typically the 30-day Treasury bill rate, although some argue it should be the rate on one-year TIPS.5 The idea was to maximize the portfolio return per unit of volatility to obtain the best “risk-adjusted” return. It should be noted that Strategy A (minimax) could also be considered a “risk-adjusted” return in the sense that it factored in the worst-case returns, not just the variability of returns.
Strategy C: maximize expected returns. Strategy C had the simple goal of maximizing average annual return, ignoring risk. This approach is often taken by advisers who ignore time segmentation issues, claiming that by generating sufficient returns, investors will be able to reach their goals without concern for risk measures. Markowitz noted that a portfolio seeking to maximize expected return would simply allocate to the single highest return asset (Markowitz 1991). This was indeed the case in the empirical investigation of Strategy C conducted here, which allocated only to small-cap value stocks, the highest returning asset class in the dataset over all 40 holding periods.
Comparing the Strategies for Various Horizons
How well did these strategies compare to each other and to the benchmark of 100 percent S&P 500 Index?
To answer this question, a large number of portfolios were constructed using Excel’s “generalized reduced gradient” nonlinear programming algorithm. Each strategy was optimized over each time horizon (120 optimizations overall), and three performance measures were tracked: (1) average (mean) return; (2) minimum return; and (3) standard deviation of the ending value.6
Each portfolio was rebalanced annually. The analysis was a historical audit to maintain the sequence of returns that actually occurred from 1928 to 2015, including the Great Depression. Data for 16 different U.S. asset classes from the CRSP and Fama/French datasets were used: S&P 500, CRSP 1-2 Growth, CRSP 1-2 Neutral, CRSP 1-2 Value, CRSP 3-5 All Midcap, CRSP 3-5 Midcap Growth, CRSP 3-5 Midcap Neutral, CRSP 3-5 Midcap Value, CRSP 6-8 All Small Cap, CRSP 6-8 Small Cap Growth, CRSP 6-8 Small Cap Neutral, CRSP 6-8 Small Cap Value, CRSP 9-10 All Microcap, CRSP 1-10 Total Market, commodities (based on CRB Index), and real estate (based on FTSE NAREIT Composite Index).7
International and emerging markets were excluded based on the assumption that some might question the accuracy for returns of these two asset classes for a study going back as far as 1928. This would be especially true for emerging markets, which are different now than they were then. A limitation on these results, therefore, is that the conclusions apply only to the portion of a portfolio allocated to U.S. equities.
Another limitation is that the goal was to find the best portfolio for each holding period based on returns over the entire timespan from 1928 to 2015. It could be that the portfolio allocations would change and produce different results if returns for 1947 to 2015 or some other starting date were analyzed. Such extensions await future research.
Results: The Equity Yield Curves
As mentioned earlier, a separate non-linear programming formulation was solved for each strategy and each time period of one year to 40 years, 120 scenarios in total. All returns are total returns, compounded annually. For time segments longer than one year, the returns were computed as compounded annualized averages within the span, but the average for all, say, 10-year spans is the simple mean, because compounding can only be done within each 10-year span.
Table 2 is the key table in this analysis. It presents performance results for each strategy and the S&P 500 Index as benchmark over five, 10, 15, 20, 25, 30, 35, and 40-year rolling timespans. Equity yield curves were quite evident for each strategy in Figure 2, which plots both averages and minimums from Table 2 including all 40 timespans.
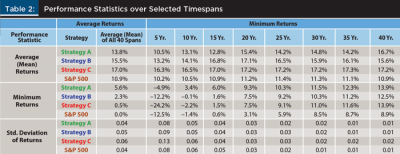
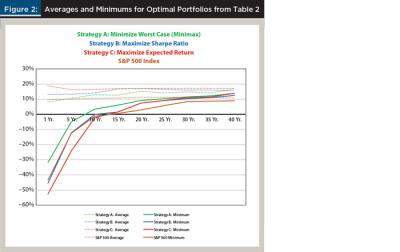
Results were as expected in all cases from one to 30 years. As is visibly shown in Table 2 and Figure 2, Strategy A (minimax) achieved the best minimums but at the expense of lower averages. Strategy C (expected return) achieved the best averages and worst minimums, and Strategy B (maximize Sharpe ratio) fell in between. This was true also for the standard deviations. For 40-year timespans, Strategy B (Sharpe) did a little worse than Strategy A in terms of average return but its standard deviation was a tie. All three strategies beat the S&P 500 benchmark in all but a few cases.
Some might wonder why the S&P 500 did not do better. These results examined something uncommon—holding periods longer than one year. Most prior research has been based on one-year holding periods, and it has been this prior research that has formed many planners’ intuitions. Building optimal portfolios based on mathematical programming (a well-known optimizing algorithm) for timespans longer than one year is arguably new and could well produce results that may seem counterintuitive. Some research questions whether a pure S&P 500 Index should be considered an efficient portfolio (Grinold 1992).
The equity yield curve for Strategy A was visibly higher than B, and B was higher than C. Standard regression analysis of the minimums against the natural log of the years (Y = a + b(lnX)) yielded adjusted R-squared values in the 90 to 95 percent range, and p-values well below 5 percent for the coefficient. However, the analysis dealt with rolling horizons with overlapping data points, meaning the data observations were not independent of each other. This violated one of the underlying assumptions in the mathematical mechanics of the econometric theory behind regression analysis, so, technically speaking, the results did not meet the standard needed to claim statistical significance.
A more complete version of Table 2 (available on request from the authors) revealed that Strategy A (minimax) reached a positive minimum return and stayed positive for all timespans longer than six years. This easily beats the other two strategies and the S&P 500—they all required 15 years to achieve this milestone. In the context of an investor’s financial plan, the minimax strategy was able to recover more quickly from stock market losses, thereby helping the portfolio to be more resilient in times of market turmoil.
Limitations of Mathematical Optimization
As shown in Table 2, Strategy C (expected return) produced average returns that were higher than the other strategies. Why not use it exclusively?
First, its worst case became significantly worse than the other two strategies. This disadvantage dwindled as the holding period extended, but never quite vanished. Some investors claim they can tolerate large swings in their portfolios, but when actually faced with large losses, they may not have the fortitude to ride through the market turmoil and, instead, sell at just the wrong time. This greater downside risk may also have a large impact on the probability of achieving their long-term financial goals, because it is low returns from poor markets that put pressure on a financial plan, not average returns.
The second and perhaps more provocative reason against exclusively using Strategy C is the fact that its mandated allocation did not follow conventional wisdom regarding diversification. As Markowitz (1991) predicted, it consisted of 100 percent small-cap value stocks over all horizons. It may be mathematically correct, but few investors would likely feel comfortable with a portfolio constructed entirely of small-cap value stocks. This lack of diversification among asset classes is a common side effect of mathematical programming. Unless constrained, optimizers blindly pursue mathematical solutions—they ignore diversification, conventional wisdom, possible end-client reactions, and other “human” factors.
Regarding allocations mandated by the mathematics for Strategies A and B, there were no easily discernable patterns; each holding period generated a different allocation for each strategy. Only Strategy C led to a single asset class allocation. The number of asset classes used changed as well, as the allocations to each asset class varied from one holding period to the next. This underlines the importance of time segmentation in building portfolios.
Strategy A (minimax) demonstrated the greatest degree of diversification in that some of the 40 different portfolios used all 16 asset classes (13-, 14- and, 17-year holding periods) while others used only two of the asset classes (five, 20, 23, 24, 29, 37, and 39 years). On average, Strategy A used 8.4 asset classes. A plot of the number of asset classes against holding period length follows what could be best described as a random walk following no distinct path. The asset class that had the largest average allocation over all 40 horizons for Strategy A was large-cap value (33.0 percent), followed by small-cap value (28.4 percent) and microcap (10.8 percent). The balance of the allocations was scattered among all the other asset classes. The asset classes that averaged close to zero allocations were the S&P 500, CRSP 1-2 neutral, midcap growth, total market, and real estate.
Strategy B (Sharpe) behaved a little better. It generated diversified portfolios for horizons shorter than 15 years, but concentrated on only two for most of the periods longer than 15 years. It used a maximum of six asset classes for one holding period (five years), five asset classes for eight holding periods (three years and six to 12 years), four asset classes for three holding periods (four, 13, and 14 years), and three asset classes for five holding periods (one, two, 18, 19, and 40 years). All other holding periods had only two asset classes, though not the same two. As expected, small-cap value and midcap value were the dominant pair in all horizons, showing up in nearly every holding period. They averaged 43 percent and 40 percent respectively over all 40 holding periods combined. Small-cap neutral (9 percent) and large-cap growth (7 percent) were in distant third and fourth places.
Future research with shorter time periods than 1928 to 2015 may reveal more discernable allocation patterns for Strategies A and B.
The Trade-Off: Average vs. Minimum Return
The minimax Strategy A should be attractive to conservative investors, because it provides the highest possible minimum returns over a given time horizon. It clarifies the consequences for investors who harbor fears that a bad market will create havoc in their lives. Basing all other calculations on a foundation of worst-case returns means any performance surprises should be pleasant, or at least better returns than other strategies. There is no guarantee that the future can never be worse than the past, of course, but an adviser facing an upset client could remind the client that the investment strategy was based on the most prudent actions possible from a historical perspective.
The downside, of course, is that this prudence comes at a price: lower average returns. In some way, the minimax strategy is like any other insurance policy—it is not free (the strategy is long only in that it uses neither hedging nor portfolio insurance strategies).
Table 2 reveals the trade-off between higher averages versus higher minimums over all horizons. For example, the expected return for a 10-year optimal portfolio based on Strategy A is 13.1 percent, but it could be as low as 3.4 percent. For Strategy B, the equivalent returns are 14.1 percent and –0.1 percent respectively. In other words, giving up 1.0 percent in average return increased minimum return by 3.5 percent in the 10-year case. Another way to say this is that to gain a 1 percent increase in the minimum, the investor would have to give up about 29 basis points in average return (1/3.5 = 0.286).
Unfortunately, this trade-off was not constant. It was fairly well behaved for horizons of 15 years or shorter. The trade-off rose slowly but steadily as the time horizon lengthened from a low of 13 bps for all two-year spans to a high of 91 bps for all 15-year spans, with an average of about 47 bps. Beyond 15 years, the pattern became quite random, averaging 122 bps.8
As expected, an adviser choosing between Strategies A or B for a client’s lifetime plan would need to know the time horizon relevant to each client as well as his or her risk tolerance. Some clients may feel that they would rather have the assurance that their equity portfolio will not cause them any problems because their entire equity portfolio has been built to withstand the worst-case scenario for their own horizon. Other clients may be willing to separate their portfolio into segments by time. Such clients may wish to use the minimax strategy for horizons of 15 years or less, and use the maximum average return strategy for 16 years or longer (assuming they could tolerate all small-cap value stocks).
The Fixed Income Component
The foregoing analysis ignored fixed income investments; it focused only on the equity component of a client’s portfolio. The equity allocation could be called the client’s “growth portfolio” because its purpose is to grow over time. Some investors in the accumulation stage may be quite happy to stop there. But for other investors who worry about losses or those approaching retirement, the role of fixed income becomes increasingly important.
The fixed income component in a portfolio is generally designed for a different purpose: stability. For retirees, it can actually serve two purposes simultaneously. Bonds can provide both stability and predictable income using what is known as dedicated portfolio theory. It consists of buying and holding individual bonds to maturity in just the right quantities and maturities so that coupon interest and redemptions combine together each year to match the income needed. Financial textbooks call this the cash matching problem. The trick for this income portfolio is figuring out the quantity of each maturity to buy so as to get the correct match. Fortunately, mathematical algorithms to accomplish this have already been developed so that the bond cash flows not only match the income stream, they do so by using the least costly set of bond portfolio needed to accomplish the task (Huxley and Burns 2004).
Conclusion and Further Research
Time segmentation can and should play an important role in developing a portfolio that aligns with an investor’s financial plan. When applied to equities, a new yield curve becomes apparent. A growth-oriented equity investment strategy to minimize the worst-case scenario rather than average or expected returns takes advantage of this phenomenon and may represent an attractive option for conservative investors. When integrated with dedicated portfolio theory on the fixed income side, the combination of the two approaches could represent a welcome response to the fear expressed most often by those near or in retirement—running out of money.
Future research should explore the nuances of dedicated portfolio theory, integrating equity portfolio strategies, sustainable withdrawal rates, and the critical path a retirement portfolio must follow to maximize the probability of lasting a lifetime. It would also be interesting to explore the robustness of these conclusions by testing them using shorter historical databases. Would the results be the same if replicated back to 1947 or some other starting date? Extensions of this research should reveal the answers to these types of questions.
Endnotes
- Technically, the YTM calculation assumes that all coupon proceeds are instantly reinvested in zero coupon bonds purchased at precisely the same rate as the original YTM.
- For animations of bond yield curves, see: businessinsider.com/us-treasury-yield-curve-evolution-1982-2014-2014-12; www.youtube.com/watchv=LZMfI5H7KCg&nohtml5=False; and youtube.com/watch?v=yph8TRldW6k.
- There is a statistically significant effect of holding period on average returns, but its effect is negligible compared to its effect on minimum returns.
- See the full text of the lecture at http://www.nobelprize.org/nobel_prizes/economic-sciences/laureates/1990/markowitz-lecture.pdf.
- The correlations between T-bills and TIPS were weak for short holding periods. But as the length of the holding period extended, the correlation tended to strengthen. For all 40 holding periods of one to 40 years, the average correlation was 0.65 with a high of 0.91 (17-year holding period), and a low of 0.15 (one-year holding period). These correlations suggest that the results for Strategy B would not likely change significantly with TIPS from those shown here, although the question suggests further research in the future.
- Maximum and median returns were also tracked but are not shown here. Maximums were rather irrelevant and were tabulated primarily as a matter of personal curiosity. Median returns had a 90 percent or higher correlation with mean returns and were thus considered redundant with the mean returns shown here.
- See the Kenneth R. French Data Library at mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html .
- Strategy A (minimax) dominated Strategy B (Sharpe), where both average and minimum returns were better for holding periods of 28 years and for holding periods of 37 to 40 years.
References
Bengen, William P. 1994. “Determining Withdrawal Rates Using Historical Data.” Journal of Financial Planning 17 (3): 172–180.
Blanchett, David, Michael Finke, and Wade Pfau. 2014. “Jeremy Siegel vs. Zvi Bodie: Does Equity Risk Decrease over Time? Advisor Perspectives, posted September 23 at www.advisorperspectives.com/articles/2014/09/23/jeremy-siegel-vs-zvi-bodie-does-equity-risk-decrease-over-time.
Grinold, Richard C. 1992. “Are Benchmark Portfolios Efficient?” The Journal of Portfolio Management 19 (1): 34–40.
Halmos, Paul R. 1973. “The Legend of John Von Neumann.” The American Mathematical Monthly 80 (4): 382–394.
Huxley, Stephen J., and J. Brent Burns. 2004. Asset Dedication. New York: McGraw-Hill Education.
Kahneman, Daniel, and Amos Tversky. 1979. “Prospect Theory: An Analysis of Decision under Risk.” Econometrica 47 (2): 263–291.
Leibowitz, Martin L. 1986a. “The Dedicated Bond Portfolio in Pension Funds Part I: Motivations and Basics.” Financial Analysts Journal 42 (1): 68–75.
Leibowitz, Martin L. 1986b. “The Dedicated Bond Portfolio in Pension Funds Part II: Immunization, Horizon Matching, and Contingent Procedures.” Financial Analysts Journal 42 (2): 47–57.
Macrae, Norman. 1992. John Von Neumann: The Scientific Genius Who Pioneered the Modern Computer, Game Theory, Nuclear Deterrence, and Much More. Providence, Rhode Island: American Mathematical Society.
Markowitz, Harry M. 1991. “Foundations of Portfolio Theory.” Journal of Finance 46 (2): 469–477.
Sharpe, William F., Gordon J. Alexander, and Jeffery V. Baily. 2001. Fundamentals of Investments, 3rd Edition. Upper Saddle River, New Jersey: Pearson.
Wald, Abraham. 1945. “Statistical Decision Functions which Minimize the Maximum Risk.” The Annals of Mathematics 46 (2): 265–280.
Young, Martin R. 1998. “A Minimax Portfolio Selection Rule with Linear Programming Solution.” Management Science 44 (5): 673–683.
Citation
Huxley, Stephen J., J. Brent Burns, and Jeremy Fletcher. 2016. “Equity Yield Curves, Time Segmentation, and Portfolio Optimization Strategies.” Journal of Financial Planning 29 (11): 54–61.