Journal of Financial Planning: June 2015
Universal or funded-goal portfolios, and simultaneous or sequential savings?
Planners must make a variety of recommendations; some with a sound theoretic basis, some based on rules of thumb or best guesses. Although the investments field has a massive research base, we often must choose between alternative investment worldviews when considering client recommendations.
There are many examples of these investment issues. How much should we hold in safe assets? Should we recommend modifying portfolio risk levels by varying the proportion of funds held in cash (the Sharpe model) or by selecting the appropriate risk levels of individual or portfolios of securities (the Markowitz model)? Should we be strategic or tactical in our asset allocation selection? When should we select from active portfolio managers and when from passive funds? And finally, how should we consider the taxability of portfolios in asset location?
Planners can come to varying conclusions on these practical decisions and yet feel justified based on sound but opposing theory. Although there is much to debate in a planner’s view of investments, some things we can all agree upon. We can agree that if you are not mega-wealthy (read Warren Buffet, seeking corporate restructuring), or you are not a technology-rich investment banking firm accomplishing micro-second arbitrage, you should diversify. We can agree that in selecting portfolios whose assets are held for a particular goal, you should consider time horizon, the importance of the goal to the client, and the client’s level of risk aversion. But are these factors, though generally acknowledged, always considered?
Universal or Distinct Portfolios?
Sometimes segregating a client’s assets by goal seems natural. Let’s assume that the 401(k), 403(b), or IRA account is for retirement (of course it isn’t always). In that case, the selection of investment assets or the allocation to asset classes is determined primarily by the time horizon to expected cash outflows and secondarily with a client’s risk preferences.
Let’s assume the purpose of a client’s 529 or Coverdale Education Savings Account is to provide for education expenses (of course it isn’t always). Again, the selection of investment assets or the allocation to asset classes is determined primarily by the time horizon to expected cash outflows. This seems simple enough. So we can agree that after selecting our theoretic investment principles addressed earlier, we have the tools to invest our client’s funds.
But as a practical matter, many planners consider that each client has a single universal portfolio designed to meet each of their needs. This has several advantages: it is administratively simpler, for one (managing separate portfolios for each client goal is clearly more complicated). Secondly, each universal portfolio can be selected based upon a client’s degree of risk aversion. And finally, holding an optimally diversified portfolio is much more easily accomplished with a single universal portfolio. Clearly these are all important factors.
On the other hand, a single universal portfolio for each client goal cannot take two important factors into account very well: (1) that the time horizon to each goal’s cash outflows differ; and (2) that a client’s risk tolerance may differ with each goal. Acknowledging these factors would require a distinct portfolio for each client goal.
How should we reconcile these two different approaches? I would say “carefully.” By that I mean we should take an eclectic approach. We could build a universal portfolio for the client, but we must modify it to take the time horizon and separate risk tolerance issues into account. Add this to the reasons financial planning is an art that is not well suited to robo-advising. Future modeling may resolve these inconsistent approaches, but we are not there yet.

Fund Goals Simultaneously or Sequentially?
Here is an additional, related issue: do we fund client goals simultaneously or sequentially?
Let’s assume our clients’ goals are not fully funded. Clients save for goals in a pattern that might be called opportunistic. When a client comes in for planning, there is no assurance that the proportion of fu nding of their retirement portfolio and education portfolios are in any way related to either their total need or their time horizon. The funding of these goals is often more a function of tax-savings opportunities and client priorities than of optimal financial planning.
If we save for goals one at a time (sequentially), one would assume we save for the nearest-term goals first. The problem with that is we will always favor time horizons near at hand. And the allocation to these shorter-term goals is therefore on the safer, low-returning side. That’s not good. So we may decide that we will have our clients save for all their goals simultaneously with the resulting riskier, higher-returning assets for the more distant goals. That’s nice, except can we accomplish simultaneous accumulation and still achieve sufficient cash flow to support our nearer-term goals in time?
Let’s use a simple example. Our 43-year-old clients have only three goals: retirement, education for their daughter, and the purchase of a new home. In addition to other resources, you have calculated they will need $800,000 at their hoped-for retirement in 24 years. You have also determined they need to have $100,000 to help provide for college education in seven years. Suppose, finally, the client wants $25,000 to buy a new home in three years so they can move to a better school district for their now 12-year-old daughter who will be starting high school at that time. A financial summary of the client’s situation is shown in the table of goals and financial data.
Although we may differ greatly regarding our capital market expectations, let’s assume our time-horizon based market expectations indicate zero- to three-year returns will be 1 percent, four- to seven-year returns will be 4 percent, and returns for horizons beyond seven years will be 7 percent. Also, to make life simple, we ignore taxes and unexpected shifts in the rate of return or inflation because that distracts from our main point.
Many would be happy with the normal computation of these annual payments (I used beginning-of-year payments with constant rates). Column five in the table above shows these amounts. Bear in mind, however, that as each of the funded-goal portfolios pass through shorter time horizons, returns should be reduced as previously indicated. Therefore the last column shows the increased payment that would be necessary to accommodate these reduced rates.
If we start to save for all goals simultaneously and immediately we would have to save very large amounts initially. As each goal is achieved, our saving would be reduced. In our example, we would need to save $8,169 per year for three years for the home purchase; $13,156 per year for seven years for the college savings; and $17,632 per year for 24 years for the retirement portfolio, assuming time-horizon reduced rates. But that probably won’t work because the clients need to save a huge amount ($38,957/year) for the first three years, and then $30,788 for the next four years, and then drop to $17,632/year until retirement. So that is not really an option.
In this case, it is also possible to save for all three goals simultaneously. If we save for all the goals at once with a constant amount, we can accomplish them all with an annual savings of approximately $26,618/year. Obviously this is preferable. It should also be observed that taking time horizons into account with their diminishing rates results in a large difference in savings needed. That is because one earns the lowest rates while their portfolios are the largest. But this strategy has significant portfolio implications.
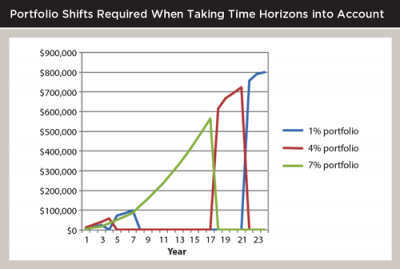
The graph above shows the nature of the portfolio shifts required when acknowledging these time-horizon issues. These shifts are substantial and may even be remarkable. The point is: if we save for all three goals simultaneously we often need to fund them in the order of their time horizon, but we need to do that and still maintain the broadly diversified, risk-tolerant portfolio for the longer-term goals because of the expected higher return for longer-term assets.
Most planners seem to use a single universal managed portfolio to help clients achieve their multiple objectives. This can often be done while incorporating time-horizon based return shifts if one is prepared to see somewhat volatile shifts in portfolio constituency. As this is often not the case, I can only conclude planners are not incorporating time-horizon issues to the fullest extent.
Financial planners can get consumed with technology: simulation modeling, sensitivity analysis, hedging, rebalancing, tax location, and others, ad infinitum. These are important and useful tools, but some unresolved issues depend on our understanding of basic financial math.
Most planners seem to agree that taking time horizons into account in building portfolios is important. Most of us agree that working to achieve client goals simultaneously has distinct advantages. It is essential to address these basic issues while also advancing to some of the more arcane aspects of client portfolio management.
Thomas Warschauer, Ph.D., CFP®, is professor of finance, emeritus, at San Diego State University Business School and program director of their financial planning programs. He served as the Journal’s first academic editor and first president of the Academy of Financial Services. Currently, he is an associate editor of Financial Services Review.
Editor’s note: For more on goals-based financial planning, see David Blanchett’s latest research in this issue.