Journal of Financial Planning: June 2015
David Blanchett, CFP®, CFA, is head of retirement research at Morningstar Investment Management. He is the 2015 recipient of the Journal’s Montgomery-Warschauer Award for his May 2014 Journal paper “Exploring the Retirement Consumption Puzzle.”
Executive Summary
- The financial planning profession is built on helping people accomplish goals. While investing appropriately is generally an important part of accomplishing a goal, achieving a goal often requires advice beyond selecting investments based on alpha and beta.
- Past research on the topic of goals-based financial planning has focused primarily on determining optimal portfolios to fund different types of goals. In contrast, the focus of this research is how to determine which goals should be funded, as well as how to optimally save toward goals over time.
- A utility model based on prospect theory was used to determine the optimal funding strategy for a household.
- The results suggest that using a goals-based framework to determine which goals to fund and how to fund them can lead to an increase in utility-adjusted wealth of 15.09 percent for a hypothetical household versus a naïve strategy focused only on funding retirement. This is equivalent to generating an annual alpha of 1.65 percent for the lifetime of the base scenario household.
Financial planning is a goals-based profession. Financial planners help clients determine how to accomplish their goals through advice and guidance on a variety of topics, such as saving, investing, and risk management. While investing well is generally an important part of the process of accomplishing a goal, achieving a goal often requires advice beyond building appropriate portfolios (beta) and selecting investments that are expected to outperform their peers on a risk-adjusted basis (alpha).
The body of research dedicated to quantifying the potential benefits of financial planning beyond alpha and beta is growing. For example, Blanchett and Kaplan (2013), using the concept of “gamma,” found that a retiree can expect to generate 22.6 percent more in certainty-equivalent income in retirement through implementing five fundamental financial planning decisions or techniques.
This paper builds on the gamma concept by determining an optimal goals-based strategy. While past research has focused primarily on determining optimal portfolios to fund different types of goals, this paper focuses on the choice of which financial goals to fund, as well as how to save for those goals over time. Certain goals, such as retirement, are decomposed where the household is assumed to have varying levels of preference with respect to replacing different amounts of income. For example, replacing 50 percent of pre-retirement income may be critical to fund nondiscretionary expenses, with the remaining levels of replacement (up to 100 percent of pre-retirement income) becoming increasingly less important.
In this study, a utility model based on prospect theory was used to determine the optimal funding strategy for a household, based on the unique prefeences and financial situation of that household. Results suggest that using a goals-based framework to determine which goals to fund and how to fund them can lead to an increase in utility-adjusted wealth of 15.09 percent for a hypothetical household versus a naïve strategy focused only on funding retirement. This is equivalent to generating an annual alpha of 1.65 percent for the lifetime of the base scenario household. These potential gains suggest a significant amount of value using a goals-based financial planning approach that extends beyond traditional asset management decisions.
Defining Financial Goals
Each person has a continuum of goals he or she would like to accomplish. Aiming to take the family out to dinner over the weekend is a goal that may require cutting back on other expenditures during the week, however this type of short-term goal is generally not included in a financial plan (although it may be discussed during the budgeting process). Financial planning goals are generally significant expenses, such as paying for college, retiring, and leaving a bequest.
Saving is how clients fund future goals too large to be included in an annual budget without a meaningful shock to consumption. For example, although some households could potentially pay for college with future earnings, it may be difficult given the significant cost of college.
The life-cycle hypothesis, originally introduced by Modigliani and Brumberg (1954), is a popular theory used to describe how individuals make financial decisions over time. According to the theory, if an individual wants to fund some level of consumption in the future but will be unable to do so with future earnings, then he or she must accumulate wealth (or take on future debt) to cover the consumption gap.
Within the life-cycle hypothesis, money is effectively a resource that should be used to purchase the set of goods from which an individual (or couple) derive the most satisfaction. Creating a goals-based financial plan is considerably complex when multiple goals are introduced, especially given resource constraints. Given the inability to fund everything a client wishes to accomplish, a financial planner must help determine which goals the client will be able to fund, as well as how to go about funding the selected goals. And while households may seek to accomplish similar goals, the magnitude and relative importance of the goals they wish to accomplish are likely to vary significantly. Therefore, each goals-based financial plan should be unique to that client.
Goals-Based Financial Planning
A growing body of research is focusing on the potential benefits of helping clients accomplish their goals. This research generally moves beyond the potential benefits of a single strategy and takes a more holistic perspective with respect to the benefit of financial planning. For example, Shefrin and Statman (2000) demonstrated that portfolios optimized using a behavioral approach will differ from mean-variance optimized portfolios. They noted that goals-based portfolios tend to combine low and high aspirations and are often depicted as layered pyramids where investors divide their current wealth between a bottom layer designed to avoid poverty (which is invested conservatively) and a top layer designed for a shot at riches (which is invested aggressively).
One goals-based approach is to create a “portfolio of sub-portfolios,” where a specific portfolio is designed to meet each specific client goal. This approach has been discussed by Brunel (2003), Nevins (2004), and Chhabra (2005). Das, Markowitz, Scheid, and Statman (2010) demonstrated that this approach can still be efficient through mental accounting, where the definition changes from the volatility of returns to the probability of failing to achieve a goal.
An alternative approach to creating a portfolio in a goals-based framework is to do so holistically. Fowler and de Vassal (2006) introduced a holistic optimization of goals approach, whereby a single investment portfolio strategy is determined that best meets the combination of client goals, and assets are then spread across different locations based on relative tax efficiency.
A variety of perspectives are being used in practice to quantify the benefit of financial planning services beyond traditional asset management metrics like alpha and beta. Bennyhoff and Kinniry (2011) called this adviser’s alpha; Scott (2012) termed this household alpha; Blanchett and Kaplan (2013) called this gamma; and Grable and Chatterjee (2014) termed this zeta. Each research term offers a different approach to quantifying the potential benefit of financial planning, yet each appears to have a relatively similar goal—to demonstrate that the potential value of financial planning cannot be captured entirely through portfolio decisions.
For example, Blanchett and Kaplan (2013) found that through implementing five fundamental financial planning decisions/techniques a retiree can expect to generate 22.6 percent more in certainty-equivalent income in retirement. This has the same impact as an annual arithmetic return increase of 1.59 percent each year during retirement. As more advisers, firms, and researchers seek to quantify the potential benefit of financial planning, we’ll likely see an increasing amount of literature on adviser’s alpha, gamma, and zeta.
A Goals-Based Utility Model
A variety of utility functions may be used to estimate the satisfaction individuals receive from varying types of consumption. The purpose of this section is to lay out a framework for a goals-based utility function that can be used to help determine how to most effectively select among different potential goals, as well as determine the optimal method to go about funding them for a client.
Certain aspects regarding the shape of a goals-based utility function are relatively straightforward. First, the utility should be higher for accomplishing goals that are more important. For example, if the client would rather fund his children’s education versus buy a new car, he should receive more utility from paying for college than from buying a new car. What is less clear is what the magnitude of the differences should be between preferences. That is, if accomplishing a goal is very important, how much more utility does the client receive from accomplishing it versus a goal that is not very important?
It is safe to assume that the utility from not accomplishing a goal at all should be zero (it’s possible the thought of funding a goal may provide some utility, but this potential benefit is ignored). Although utility should increase as the percentage of the goal is increased, it is less clear what the shape of the utility function should be. In other words, what is the marginal benefit of moving toward certainty with respect to accomplishing a goal?
The Constant Relative Risk Aversion (CRRA) utility function is one of the most common models used to quantify preferences. The CRRA utility function has a concave shape, which implies diminishing marginal utility. Diminishing marginal utility means that while each additional unit of consumption makes an individual happier, the rate in the increase of satisfaction decreases. For example, if someone is very thirsty, one cup of water will make the person very happy. An additional cup of water would likely also lead to happiness but with less effect than the first.
The CRRA utility function is shown in equation 1, where utility (u) is a function of a given level of consumption (c) based on the individual’s level of risk aversion (γ):

From a goals-based perspective, a problem with a CRRA utility function is it implies that the majority of utility achieved from accomplishing a goal (assuming that c is substituted for the percentage of the goal completed in equation 1) can be obtained from partially completing the goal. For example, if a risk aversion level (y) of 4 is assumed, approximately 80 percent of the total utility from accomplishing a goal would be obtained from only accomplishing 50 percent of the goal. Therefore, if a client is faced with multiple goals but lacks the resources to fully fund all of them, a CRRA utility approach would imply the client should partially fund each goal rather than choosing to fully pursue certain goals. Taken to the extreme, an individual would only fund a goal if all the other goals were also fully funded. This seems inconsistent with how most people would choose to allocate resources when faced with competing goals and limited resources.
Heath, Larrick, and Wu (1999) suggested that goals serve as reference points. These points systematically alter the value of outcomes as described by the psychological principles in prospect theory’s value function (Kahneman and Tversky, 1979).
The prospect theory utility function has three important properties: (1) it defines gains and losses with respect to a reference point; (2) it is concave in gains and convex in losses; (3) and it is steeper for losses than gains. The natural reference point in a goals-based framework is goal completion. Convexity below the reference point (completing the goal) suggests that individuals derive an increasing amount of satisfaction as they move toward goal completion, which is consistent with research by Hull (1932), who noted a tendency for animals to become more motivated as they approach a goal. Heath et al. (1999) also demonstrated this effect through surveys.
Concavity above the reference point also seems consistent with goal accomplishment, as the relative utility from overfunding a goal should diminish. De Giorgi (2011) used a model based on prospect theory to determine the optimal funding strategy for different goals. Results supported this notion.
The prospect theory utility function equation introduced by Tversky and Kahneman (1992) is shown as equation 2, where utility (u) achieved from an outcome (x) is a function of the coefficient of loss aversion (λ), the gain satiation coefficient (α), and the loss satiation coefficient (β). It is generally assumed that 0 < α < 1, 0 < β < 1, and 2 < λ < 4, and that α = β. Tversky and Kahneman suggested λ = 2.25, α = 0.88, and β = 0.88.
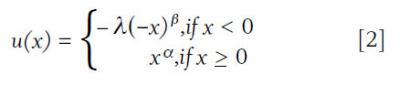
The traditional prospect theory utility equation can be adjusted to provide insight into the utility achieved from completing a goal based on equation 3 where utility (u) is a function of the percentage of the goal completed (c%). For example, if the goal is to save $50,000 in 10 years, and the individual is able to save $30,000, the goal completion percentage would be 60 percent. It is also possible to add a preference factor (p), which is assumed to be the relative preference of the individual for completing a goal. Preference is an important consideration because goals often differ in their importance.
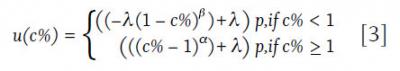
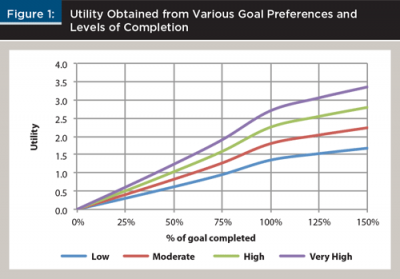
For this analysis, and consistent with Tversky and Kahneman (1992), it is assumed that α = 0.88, α = β, and λ = 2.25. In this study, it was assumed that p equals 0.6, 0.8, 1.0, and 1.2 for goals that are of low importance, moderate importance, high importance, and very high importance, respectively. The p coefficient values are subjective and were selected so that there would be a meaningful difference between different levels of relative importance. The resulting utility from varying goal preferences and levels of completion is shown in Figure 1.
This approach can be used in a stochastic setting to determine the utility achieved from different potential funding decisions. Within each run, the utility from the percentage of the goal completed (equation 3) can be determined, where the average utility across all runs is the assumed certainty-equivalent value, or completion percentage, for the entire scenario.
To make the goals relative, especially those that occur over multiple periods, the net present value of each goal was estimated using a real discount rate of 2 percent. If an individual has a higher subjective discount rate, this preference with respect to a goal would manifest itself via the preference factor in the current model, although an alternative approach would be to incorporate it in the discount rate.
The total utility achieved from accomplishing each goal can be obtained by multiplying the net present value of the cost of the goal by the certainty-equivalent goal completion percentage. The total utility achieved across all goals would be the summation of these values—this is called the utility-adjusted completion score. The goal for each individual would be to maximize the utility-adjusted completion score.
Hypothetical Scenario
To quantify the potential benefits of a goal-based approach to financial planning, the following hypothetical scenario was created. The scenario is based on a married couple, both age 30. They have two children ages 3 and 5. The total assumed pretax annual income for the household is $120,000, which can be decomposed as $90,000 from the primary worker and $30,000 from the spouse. Total compensation is assumed to increase by 0.5 percent per year, in real terms, until retirement at age 67. The household is assumed to have 20 percent of pretax income available to save or use to fund other goals. The effective ordinary income tax rate is assumed to be 20 percent. The assumed employer match available in the 401(k) plan is 50 percent on the first 6 percent of deferrals. All 401(k) monies are assumed to be pretax, and the existing total 401(k) balance is $50,000. Taxes from the 401(k) account are assumed to be paid only upon distribution at retirement.
Three types of investible accounts are assumed for the analysis: (1) a 401(k) account (as noted previously); (2) a 529 college savings account; and (3) a taxable account. The monies in the 401(k) account are assumed to be used only to fund retirement or to cover the bequest goal. The 529 monies are assumed to be used primarily to fund college; however, similar to the 401(k), the account could also be used to satisfy the bequest goal. The taxable monies could be used to fund any of the goals.
The bequest goal is to have $200,000 in today’s after-tax dollars. The funds are assumed to be available at death (age 95 for both spouses). An assumed 30 percent penalty—to reflect potential taxes and/or nonqualified distributions—is assumed if any 529 or 401(k) assets are used to fund the bequest goal. The maximum value assumed for the bequest goal is two times the target value. For the purposes of this study, real estate assets are ignored.
The taxable account is assumed to have a total current balance of $50,000. Opposed to modeling on an ongoing basis, the expected return for the account is reduced each year to reflect the potential impact of tax drag. For equities, the assumed annual return is reduced by 15 percent, which implicitly means that all gains are realized annually and taxed at the long-term capital gains rate. For cash, the annual return is reduced by 20 percent to reflect annual taxation at ordinary income rates. The fees for the 401(k) account, 529 plan, and taxable account are assumed to each be 0.5 percent annually.
The analysis assumes two investible asset classes: stocks and cash. Stocks have an annual assumed return of 9.0 percent and a standard deviation of 20 percent. Cash has an annual assumed return of 3.0 percent and standard deviation of 0 percent (i.e., cash is assumed to be a risk-free asset). The correlation between equities and cash is assumed to be zero, and inflation is assumed to be 2.5 percent per year.
The return assumptions are based off the 2014 Ibbotson long-term capital market assumptions. The entire analysis is in real terms, so all monies are adjusted to today’s dollars. The base scenario assumes the 401(k) is invested in an 80 percent stock portfolio, where the equity allocation decreases by 1 percentage point per year for the entire simulation; that the 529 is invested in a 60 percent stock portfolio, where the equity allocation decreases by 3 percentage points per year for the entire simulation; and the taxable account is assumed to be invested in a 20 percent stock portfolio for the entire simulation.
The household is assumed to have credit card debt of $20,000. The annual interest rate on the credit card debt is 20 percent. The minimum annual payment is 36 percent of the balance or $300, whichever is greater.
The retirement income goal is to replace 90 percent of post-tax, post-savings compensation at age 67. Social Security retirement benefits are assumed to commence upon retirement (age 67). Benefits are based on the average historical earnings history of the individuals and the 2014 bend points. The after-tax Social Security retirement benefits for the analysis are approximately 60 percent of the post-tax retirement goal need, which leaves the remaining 30 percent to be funded with savings. The after-tax value of the Social Security retirement benefits is assumed to be 90 percent of the forecasted value. Retirement is assumed to last until age 95.
College is assumed to cost $25,000 per year and to last for four years, where the first child starts in 13 years and the second child starts in 15 years. College costs are assumed to increase at a rate that is 2 percentage points higher than inflation. The current 529 plan balance is assumed to be $25,000.
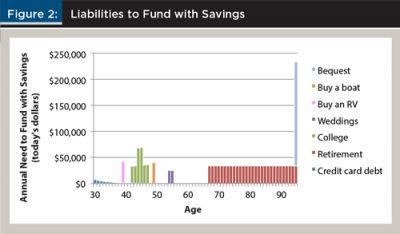
Apart from the retirement, college, and bequest goals, three lifestyle goals are assumed: goal 1, weddings, which are expected to cost $25,000 each and occur 25 and 26 years into the future; goal 2, buying an RV, which is expected to cost $40,000 in 10 years; and goal 3, buying a boat, which is expected to cost $40,000 in 20 years.
Figure 2 includes the annual required monies by age required to fund the seven goals. Note, these are the liabilities that must be funded through savings; the actual cost of retirement is higher, but the majority of the retirement need is covered from Social Security retirement benefits.
The retirement goal is assumed to have varying levels of preference; that is, certain levels of retirement income are very important, while some are less important. This approach effectively distinguishes expenses between discretionary and non-discretionary so that an individual may decide to fund certain preretirement goals (with a higher goal preference) at the cost of additional retirement income (which may have a lower preference). The retirement income goal is assumed to be a very high preference for the first 55 percent of the retirement income goal, a high preference for the next 20 percent of the retirement income goal, a moderate preference for the next 15 percent of the retirement income goal, and a low preference for the final 10 percent of the retirement income goal. The relative preference for the college, the three lifestyle goals (goal 1, goal 2, and goal 3), and bequest goals are very high, high, low, moderate, and moderate, respectively.
Scenario Solver
Given the hypothetical scenario, it is possible to determine which goals the household should fund and how the household could go about funding each respective goal from a savings perspective. The optimal strategy was determined by iterating through different potential combinations of whether to fund certain goals and then how to save toward them. The retirement and bequest goals were assumed to be attempted for all simulations (especially the bequest goal, as it represented merely residual assets at death), while the other four goals may or may not be attempted depending on which combination maximizes household utility.
There were 150 different savings scenarios and 16 different funding scenarios considered for the analysis (for a total of 2,400 scenarios). It was assumed the household saved up to the employer match (6 percent of total pretax compensation) in the 401(k) plan. The remaining savings was divided among the 401(k) plan, 529 plan, and the taxable account. Additionally, there were two credit prepayment scenarios: one where all excess savings (above the amount required to receive the maximum employer match) was directed toward paying off credit card debt and the other where only minimum payments were made.
A waterfall approach was used for directing savings, where after college was completed, the monies thereafter were either saved in the 401(k) plan or taxable account. That is, no further monies were directed to the 529 plan. The taxable account was assumed to fund goals pro rata across the analysis. For simplicity purposes, no borrowing was allowed for goal funding. In reality, loans are commonly used to fund some goals, such as education; however, introducing this would add complications beyond the scope of the analysis. Also, given the assumed fixed amount of monies to dedicate toward saving, future loan repayments would result in lower savings rates for the household. Each scenario was based on a 500 run Monte Carlo simulation.
Various naïve strategies were considered. The first naïve strategy assumed that the household was only concerned with funding retirement. No other goals were considered. Under this strategy, the household was able to fund 94 percent of its retirement goal, on average, and 153 percent of its bequest goal. The second naïve strategy assumed the household attempts to fund all goals and to follow a relatively simplistic savings strategy.
Results
Figure 3 includes information about how optimal savings should be directed annually based on the goals and resources of the household in the hypothetical scenario. There are some important differences in the recommended savings strategy versus common recommendations from financial planning engines. First, although it is common to suggest individuals maximize their 401(k) plan contributions, the optimal recommendation was as follows: initial monies beyond the employer match contribution level should be used to pay off existing credit card debt for the first two years. This recommendation makes sense from a total wealth perspective because the effective cost of maintaining credit card debt is generally higher than the potential benefit that can be achieved through saving additional monies in a 401(k) plan.

Second, once the credit card was paid off, all monies beyond the employer matching contribution were directed toward saving for college. Funding college is a very important goal for the household, and saving money in a 529 plan is an efficient means to fund this goal because all growth in the monies inside the 529 plan used to pay for college expenses are tax-free.
Finally, even after the college goal is funded, the taxable account receives a larger relative increase in savings than the 401(k) plan. This is because the individual has goals that will be incurred before retirement that cannot easily be funded with the 401(k) plan.
Figure 4 provides some perspective on the relative utility that can be obtained from different types of scenarios. Recall that the naïve approach was assumed to be when the household attempts to fund only the retirement goal.
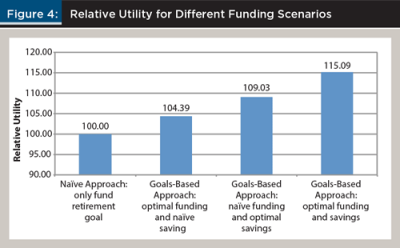
There are clear potential improvements in utility-adjusted wealth from implementing a goals-based strategy, where the optimal strategy creates 15.09 percent more utility-adjusted wealth than the naïve approach. It is worth noting that the second naïve approach, which is not included in Figure 4, where the household was assumed to attempt funding all goals was more efficient than attempting to fund only retirement. If this were the assumed naïve approach, the most efficient strategy would only generate 10.98 percent higher utility-adjusted wealth. The most efficient strategy assumes the household follows the savings strategy outlined in Figure 3, and attempts to fund all goals except goal 2, the RV purchase.
It is important to note that the potential benefits of any type of goals-based approach will vary based on the unique preferences and goals for each household. Also, similar to the output of a mean-variance optimization, the recommendation may need to be constrained for reasonableness purposes; however, this type of analysis provides a unique solution on how to go about funding goals and which goals to potentially fund.
Looking at Value from a Fee Perspective
An alternative perspective when viewing the potential increases in utility-adjusted wealth values in Figure 4 would be to determine the alpha equivalent values by looking at the increase in forecasted returns (holding risk levels constant) that would result in the same level of utility had the goals-based approach not been used. This type of analysis provides information about the potential value of financial planning from a fee perspective. For this analysis, a simulation was conducted where the return for each of the portfolios was increased from 0.0 percent per year to 7.0 percent per year in 0.25 percent increments. The resulting changes in relative utility for the first naïve strategy are shown in Figure 5.
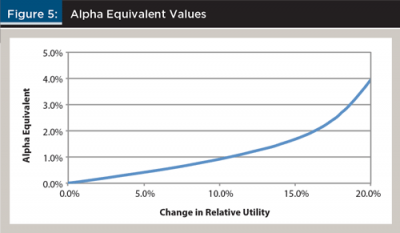
A fourth-order polynomial trend line was fit to the alpha equivalent values in Figure 5 (the R² of the trend line was 99.92 percent). Using the polynomial, it was determined that a 15.09 percent increase in utility has an alpha equivalent of 1.65 percent per year. In other words, to generate the same improvement in utility from an optimal goals-based strategy, an individual would need to create an excess risk-free return of 1.65 percent for each year of the simulation (which is 65 years). The second naïve strategy, which resulted in a 10.98 percent increase in utility-adjusted wealth, had an alpha equivalent of 1.07 percent.
The Goals-Based Financial Planning Process
The process for goals-based financial planning is depicted in Figure 6. The first step is to define the client’s goals. Next, resources that can be used to help fund the goals should be identified. Although some may contend that resources should be identified first, it’s really the goals that will and should drive the financial plan. It is unlikely clients will be able to accomplish all of their goals, but it helps to understand what is important to each client before understanding the means available to fund the goals.
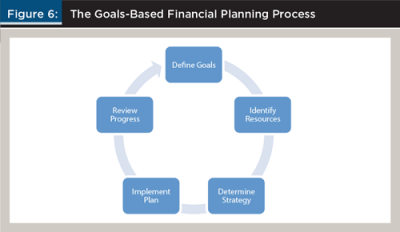
After the goals have been defined and the resources have been identified, the optimal strategy must be determined. Determining the strategy may require revisiting the resources available, as well as the goals. For example, if the optimal strategy is not consistent with the client’s wishes, it may result in the client having to save more than originally planned.
After the plan has been determined it should be implemented. This may require opening up new accounts and making potentially significant changes in how savings are directed. This is a dynamic process that should be reviewed annually and upon any major life changes. An individual’s goals and resources are likely to change over time, and the strategy should be updated to reflect these changes.
Implementing the Process
Implementing a goals-based financial planning approach may require a financial planner to take a different perspective when working with clients. The following points are potential considerations that should be addressed by anyone considering using a goals-based approach:
Change the focus. A goals-based financial planning process is focused on accomplishing a goal. This is a different focus than, say, building portfolios that outperform some benchmark. This approach may require changing the information that is relayed to the client. One example is to change the emphasis on client communication away from a focus on performance to goal completion.
Take a total wealth perspective. Nearly all clients have a variety of goals, and it takes a collective approach to accomplish each goal. This requires taking a total wealth perspective on both assets and liabilities in order to understand the total resources available to the client, as well as the potential limitations.
Think outside the portfolio. Although some goals can be accomplished through investments alone, being knowledgeable and open to non-portfolio solutions, such as annuities, can provide clients with a wider range of potential options. It is important that financial planners do not generalize a product or approach and dismiss a strategy without understanding the respective benefits and disadvantages.
Become a behavioral psychologist. Most planners have examples of clients behaving financially irrationally. Understanding why clients make irrational choices and how to “nudge” clients to make better decisions can help clients accomplish their goals.
Behavioral research suggests that goal attainment can be best achieved through first establishing a concrete goal and then setting achievable short-run goals that over time produce the long-run goal. For example, a client may set a goal of reducing credit card debt or total spending by $500 a month. In addition, automatic savings techniques that do not require active saving can be used to ensure that the client does not feel the impact of the reduction. Salary deferral or scheduled electronic transfers from a liquid account into a savings account may be more effective than relying on the long-term goal to motivate clients to make active saving decisions.
Correctly conceptualize risk. When thinking about risk, it is common to focus on risk preference or how a client feels about taking risk, which is commonly proxied through a risk tolerance questionnaire. The other important component of risk is risk aversion, which is the amount of risk an individual should take given available resources.
Build smarter portfolios. It may be operationally simple to have a single allocation for each equity risk level, but in reality, different goals have different risks that should be incorporated into the portfolio optimization routine. For example, a younger individual may be interested in maximizing return per unit of risk, and an older individual may be more focused with maximizing return per unit of risk after considering inflation. These two different approaches can lead to materially different portfolio allocations.
Incorporate new technology solutions. Implementing a goals-based approach requires that a financial planner incorporate a variety of new technology solutions for things like determining how to optimally fund goals, how to build efficient portfolios over time, how to monitor progress, as well as how to communicate all this to clients. As such, an active interest in technology solutions is necessary to fully capture the benefits of goals-based planning.
Conclusion
A utility model based on prospect theory was presented here to help planners determine the optimal funding strategy for a household, based on the unique preferences and financial situation of that household. The optimal strategy provides guidance on which goals should be funded, as well as how to save toward those goals over time. Certain goals, like retirement, can be decomposed where the household is assumed to have varying levels of preference with respect to replacing different amounts of income.
The results of the analysis suggest that using a goals-based framework to determine which goals to fund and how to fund them can lead to an increase in utility-adjusted wealth of 15.09 percent versus a naïve strategy. This is equivalent to generating an annual alpha of 1.65 percent for the lifetime of the base scenario household. These potential gains suggest there is a significant amount of value using a goals-based financial planning approach that extends beyond traditional asset management decisions.
References
Bennyhoff, Donald, and Francis Kinniry. 2011. “Advisor’s Alpha.” Vanguard Research Paper (December).
Blanchett, David, and Paul Kaplan. 2013. “Alpha, Beta, and Now… Gamma.” Journal of Retirement 1 (2): 29–45.
Brunel, Jean. 2003. “Revisiting the Asset Allocation Challenge through a Behavioral Finance Lens.” Journal of Wealth Management 6 (2): 10–20.
Chhabra, Ashvin. 2005. “Beyond Markowitz: A Comprehensive Wealth Allocation Framework for Individuals.” Journal of Wealth Management 7 (4): 8–34.
Das, Sanjiv, Harry Markowitz, Jonathan Scheid, and Meir Statman. 2010. “Portfolio Optimization with Mental Accounts.” Journal of Financial and Quantitative Analysis 45 (2): 1–24.
De Giorgi, Enrico G. 2011. “Loss Aversion with Multiple Investment Goals.” Mathematics and Financial Economics 5 (3): 203–227.
Fowler, Gordon B., and Vladimir de Vassal. 2006. “Holistic Asset Allocation for Private Individuals: Simultaneously Solving for an Optimal Asset Allocation Given the Multiple Goals and Multiple Locations of Private Clients.” Journal of Wealth Management 9 (1): 18–30.
Grable, John, and Swarn Chatterjee. 2014. “Reducing Wealth Volatility: The Value of Financial Advice as Measured by Zeta.” Journal of Financial Planning 27 (8): 45–51.
Heath, Chip, Richard Larrick, and George Wu. 1999. “Goals as Reference Points.” Cognitive Psychology 38 (1): 79–109.
Hull, Clark L. 1932. “The Goal-Gradient Hypothesis and Maze Learning.” Psychological Review 39 (1): 25-43.
Kahneman, Daniel, and Amos Tversky. 1979. “Prospect Theory: An Analysis of Decision under Risk.” Econometrica 47 (2): 263–291.
Modigliani, Franco, and Richard Brumberg. 1954. “Utility Analysis and the Consumption Function: An Interpretation of Cross-Section Data.” In Post-Kenyesian Economics, edited by Kenneth K. Kurihara, 388-436. New Brunswick, NJ: Rutgers University Press.
Nevins, Daniel. 2004. “Goals-Based Investing: Integrating Traditional and Behavioral Finance.” Journal of Wealth Management 6 (4): 8–23.
Scott, Jason S. 2012. “Household Alpha and Social Security.” Financial Analysts Journal 68 (5): 6–10.
Shefrin, Hersh, and Meir Statman. 2000. “Behavioral Portfolio Theory.” Journal of Finance and Quantitative Analysis 35 (2): 127–151.
Tversky, Amos, and Daniel Kahneman. 1992. “Advances in Prospect Theory: Cumulative Representation of Uncertainty.” Journal of Risk and Uncertainty 5 (4): 297–323.
Citation
Blanchett, David. 2015. “The Value of Goals-Based Financial Planning.” Journal of Financial Planning 28 (6): 42–50.