Journal of Financial Planning: May 2012
Michael A. Guillemette is a doctoral candidate in the Department of Personal Financial Planning at Texas Tech University. He cowrote a book chapter on risk tolerance and worked as a summer associate at Fox, Joss & Yankee, a financial planning and investment management firm, in 2009. (m.guillemette@ttu.edu)
Michael Finke, Ph.D., CFP®, is an associate professor and Ph.D. coordinator in the Department of Personal Financial Planning at Texas Tech University. His research interests include behavioral personal finance, retirement income planning, investor risk tolerance, and mutual fund performance. He is the editor of the Journal of Personal Finance. (michael.finke@ttu.edu)
John Gilliam, Ph.D., CFP®, CLU, is an assistant professor in the Department of Personal Financial Planning at Texas Tech University. His academic life is strongly influenced by more than 30 years working as an insurance and financial adviser. Gilliam currently serves on the national board of the Society of Financial Service Professionals. (john.gilliam@ttu.edu)
Executive Summary
- The literature on risk tolerance overwhelmingly justifies the use of questionnaires based on validity and reliability or psychometric testing, but there has been little research examining the relation between questions and actual investor portfolio behavior
- This study examines risk tolerance questions based on economic theory, prospect theory, and client self-assessment to determine the extent to which they explain variation in portfolio allocation preference and recent investment changes
- We conclude that risk tolerance questions based on loss aversion and self-assessment should be used when determining the portfolio allocation of clients
- While questions based on economic theory should theoretically be the best measure of a client’s portfolio allocation preference, the results of this study indicate that these questions are not very useful when both loss aversion and self-assessment questions are included in a risk tolerance questionnaire
- Planners should begin to reassess the risk tolerance level of their clients around age 60, as there is evidence that risk tolerance declines later in life because of cognitive decline
A variety of risk assessment surveys is used by financial planners to determine appropriate portfolio recommendations for their clients. The literature on risk tolerance often focuses on validity and reliability or psychometric testing of questions when evaluating the relative merits of a risk tolerance questionnaire (Callan and Johnson 2003; Grable and Lytton 2003; Hallahan, Faff, and McKenzie 2004; Roszkowski, Davey, and Grable 2005). Psychometrics includes tests for validity and reliability, but often involves an analysis of the consistency of correlations among questions in the survey. However, most risk tolerance questionnaires contain questions with no clear link to risk tolerance theory, and there has been little research examining the relation between questions and actual investor portfolio behavior.
The purpose of this study is to take a closer look at common risk tolerance assessment questions and sort them based on the risk tolerance theory they most closely resemble. The two primary theories related to risk tolerance are conventional economic theory, which views risk tolerance as the willingness to accept greater variation in outcomes, and prospect theory, which assumes investors place a greater weight on losses from an arbitrary starting point. We then compare answers given to risk tolerance questions based on conventional economics and prospect theory with self-assessment questions to determine which types of risk tolerance measures are most likely to capture a client’s actual portfolio allocation preference. The findings of this study should provide planners a better understanding of how different risk tolerance questions may predict client response to market risk in order to more accurately align portfolio recommendations with client preferences.
Literature Review
Financial advisers are concerned with recommending portfolios clients can live with during good times and bad. There is evidence that individual investors compromise long-run dollar-weighted portfolio performance by shifting their portfolios away from stocks after a drop in the market and into stocks after recent gains (Wang 2011). Pulling money out of stocks during a recession and investing more in the market during an expansion results in significant market underperformance because investors are buying when stock valuations are high and selling when valuations are low. Winchester, Huston, and Finke (2011) find that individuals who use a financial planner are more likely to maintain their portfolio during a recession; however, it is unclear whether this is because of more appropriate portfolio recommendations from accurate risk tolerance assessment, or whether planners are better able to counsel clients to moderate their loss-averse tendencies by maintaining a portfolio that aligns with their preferences.
The economic concept of risk tolerance may best be conceptualized as the willingness to accept variation in spending over time (Hanna, Fan, and Chang 1995). Modigliani and Brumberg (1954) note that individuals who are risk averse will prefer a smoother consumption path to variation in consumption during their lives. Preference for smoother consumption also leads investors to prefer assets whose payout is more certain and less volatile because volatility implies a broader range of possible future payouts. This insight is fundamental in modern portfolio theory (Markowitz 1952; Sharpe 1964). For this reason, assets that are more volatile are valued less by investors who are risk averse. Individuals with greater levels of risk aversion require a greater risk premium to invest in assets that are more volatile. The degree of risk aversion determines the optimal mix of risky and risk-free assets within an investor’s portfolio.
Risk tolerance in the capital asset pricing model (CAPM) assumes that the capital market places greater value on assets with lower variance in returns. This preference for reduced variance in random returns is commonly explained using expected utility theory. The Arrow (1965) and Pratt (1964) coefficient of relative risk aversion is consistent with the economic concept of relative preference for a stable consumption path. Changes in income have been shown to be associated with expected changes in consumption (Campbell and Mankiw 1989). Zeldes (1989) derives a numerical technique to provide accurate approximations of the consumption function with income uncertainty in multi-period models. The most widely cited Arrow-Pratt measure of risk aversion is a set of questions included in the Health and Retirement Study (HRS) (Barsky et al. 1997):
Suppose that you are the only income earner in the family, and you have a good job guaranteed to give you your current (family) income every year for life. You are given the opportunity to take a new and equally good job, with a 50-50 chance it will double your (family) income and a 50-50 chance that it will cut your (family) income by X%. Would you take the new job?
The coefficient of relative risk aversion can be estimated from responses to the HRS questions. Households with greater levels of risk aversion should prefer less consumption variance, and, because future income determines future consumption, income variation should accurately capture willingness to accept different consumption paths.
Rabin (2000) and Rabin and Thaler (2001) show that human behavior cannot be easily reconciled with traditional economic theory. People tend to care less about how risky outcomes affect utility from consumption and more about the pain they feel about losses. For example, the demand for substantial amounts of low-deductible auto insurance and noncatastrophic health insurance translates into improbable Arrow-Pratt risk aversion levels over larger stakes (Rabin 2000). Prospect theory modifies expected utility theory by overweighting the disutility experienced from losses below an arbitrary reference point, otherwise known as loss aversion. Individuals tend to be more sensitive to reductions in their levels of wealth from, say, the amount they initially invested or the amount on their most recent quarterly statement. Tversky and Kahneman (1992) estimate that losses have approximately 2.25 times the impact on an individual’s perceived welfare than an equal dollar amount of gains. The size of the equity premium is consistent with prospect theory if investors are loss averse and check their statements every year (Benartzi and Thaler 1995). A higher degree of loss aversion is associated with a lower probability of participation in equity markets and a lower allocation of wealth to equity (Dimmock and Kouwenberg 2010).
Questions from common risk tolerance scales tend to measure either risk aversion or loss aversion, or they simply ask how much investment risk respondents are willing to take. Hanna and Lindamood (2004) present a series of hypothetical pension-gamble questions in order to measure the economic concept of risk aversion. Their questions are similar to the income-gamble questions used in the HRS, except the range in which risk aversion can be measured is increased, and they clarify that once a choice is made the participant will have to live with that outcome forever. They also include graphical representations of the possible outcomes for each question for simplification purposes.
Grable and Lytton (1999) use a 20-question financial risk tolerance assessment that includes two questions based solely on prospect theory:
- In addition to whatever you own, you have been given $1,000. You are now asked to choose between:
a. A sure gain of $500
b. A 50 percent chance to gain $1,000 and a 50 percent chance to gain nothing - In addition to whatever you own, you have been given $2,000. You are now asked to choose between:
a. A sure loss of $500
b. A 50 percent chance to lose $1,000 and a 50 percent chance to lose nothing
Although the expected values of each of these questions are the same, individuals are more likely to accept the gamble in question two compared with question one. This is because of the certain outcome being framed as a “sure loss” in question two versus a “sure gain” in question one. The different reactions to gain and loss frames are often referred to as the reflection effect (Kahneman and Tversky 1979). According to Grable and Lytton (1999), choosing the sure gain in question one and the gamble in question two would indicate a person with moderate risk tolerance. Individuals who choose the certain outcome for both questions would be considered to have a low level of risk tolerance. If the gambles are chosen in both cases they would be considered to have a high level of risk tolerance.
There is evidence that clients’ assessment of their own risk tolerance may be useful when constructing a risk tolerance questionnaire. Roszkowski and Grable (2005) find that having clients assess themselves may be beneficial when advisers are assessing risk tolerance. The magnitude of the correlations between self-estimated and actual risk tolerance is “quite high” for clients relative to their ability to estimate other personality characteristics. When analyzing client self-ratings, the question with the most predictive power for risk tolerance assessment is: What degree of risk have you assumed on your investments in the past? (Answer options: 1 = very small, 2 = small, 3 = medium, 4 = large, 5 = very large).
To better understand the usefulness of questions measuring economic risk tolerance, loss aversion, and self-assessed risk tolerance, we use results from a common risk tolerance questionnaire to compare responses with actual portfolio behavior following the global economic crisis of 2008. Our results provide insight into the association between risk tolerance measures and revealed portfolio risk preference.
Changing Risk Tolerance
There has been little research conducted on whether the risk tolerance of clients should be reassessed over time. The preponderance of evidence suggests that risk preferences are relatively stable. Sahm (2007) finds that 73 percent of the systematic variation in measured risk tolerance is associated with things that do not change over time. Sahm also finds that an improvement in macroeconomic conditions is associated with an increase in risk tolerance, and that our willingness to accept investment volatility declines in old age. Roskowski and Davey (2010) present data on risk tolerance before and after the global financial crisis of 2008, showing a decline in risk tolerance that is relatively small. More pronounced is the public’s perception of an increase in the risk inherent in investing. Fortunately, perception can be altered by a client’s financial planner.
Boyle, Lei Yu, Buchman, Laibson, and Bennett (2011) find a lower level of cognitive ability is associated with lower risk tolerance in a sample of 369 U.S. adults between the ages of 60 and 98. The decline in risk tolerance in old age may be related to the natural decline in the ability to retrieve information and place it into context late in life. Financial decision making requires both memory and problem-solving skills and appears to decline significantly in advanced age (Finke, Howe, and Huston 2011). A survey of literature on behavioral finance issues affecting seniors describes how retirees display “hyper loss aversion” (Kasten and Kasten 2011). AARP and ACLI (2007) find that retirees are up to five times more loss averse than the average person. Given the evidence that risk tolerance declines in advanced age, we recommend that planners begin to reassess client risk tolerance around age 60.
Data
FinaMetrica’s Risk Profiling System is used by both domestic and international financial planners to aid them in determining the risk tolerance level of their clients. FinaMetrica’s questionnaire includes 25 risk tolerance questions. The survey includes questions that capture portfolio allocation preference and recent investment changes as well as demographic and socioeconomic information. Data were collected by Kiplinger between November 2009 and October 2010. A total of 2,050 participants answered all of the questions used in this study. The average age of the participants is 56, with 62 percent having a net worth of at least $500,000.
Operationalization of Variables
Based on the three primary ways to measure risk tolerance, we sort questions from the FinaMetrica survey and develop three measures. The first measure is based on economic theory and will be referred to as the “Arrow-Pratt” measure. The second measure is based on prospect theory and will be referred to as the “loss aversion” measure. The third measure is based on self-assessment and will be referred to as the “self-assessment” measure.
Table 1 displays the composition of the three risk tolerance measures. A summation of two questions is used to construct each of the proxies for the Arrow-Pratt, loss aversion, and self-assessment measures. The questions used for the Arrow-Pratt measure capture willingness to accept variation in consumption. The loss aversion questions gauge whether individuals focus on losses or gains and the extent to which they can tolerate financial losses. The self-assessment questions ask individuals the degree of risk they have taken with their financial decisions in the past and present periods. The scales for each of these measures range from 2 to 10, with 2 being either least willing to accept variation in consumption, most loss averse, or willingness to accept a small degree of financial risk in the past and present periods. A 10 on the scale represents the greatest willingness to accept variation in consumption, the lowest loss aversion level, or willingness to accept a very large degree of financial risk in the past and present periods.
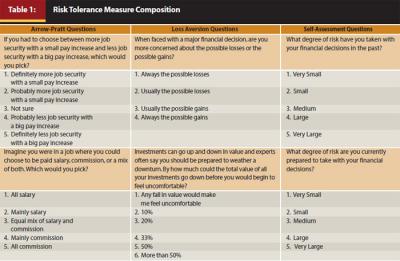
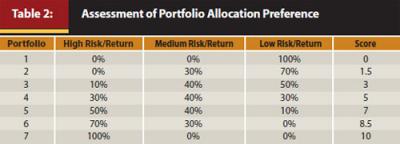
Table 2 contains a question with seven portfolio choices used to measure the effectiveness of the three measures on how well they explain variation in portfolio allocation preference. Each portfolio was given a score because moving from one portfolio choice to the next does not always have an equal effect on an individual’s preferences. The score was calculated by multiplying the high risk/return, medium risk/return, and low risk/return percentages by 10, 5, and 0, respectively.
Even more helpful to planners is the fact that these measures are tested against a question asking participants how their investments have changed in recent years:
In recent years how have your personal investments changed?
1.Always toward lower risk
2.Mostly toward lower risk
3.No change
4.Mostly toward higher risk
5.Always toward higher risk
Because the data were collected in 2009 and 2010, this question most likely captures investment changes made during the global financial crisis.
The control variables used in this study are sex, marital status, education, age, income, and net worth. Age is categorized as a continuous variable in the regression analysis. Dummy variables were created for the remaining variables with female, not married, no university degree, income less than $50,000, and net worth less than $200,000 as the reference groups. Bajtelsmit and VanDerhei (1997) find significant differences in the investment of pension assets between men and women. Using data on 20,000 management-level employees for a single U.S. firm, they find women are significantly more likely than men to allocate to fixed-income alternatives and significantly less likely to invest in employer stock. Christiansen, Rangvid, and Joensen (2010) find that women increase their proportion of wealth invested in stocks after marriage, whereas men exhibit the opposite behavior. Whether a participant has a university degree or higher qualification is a proxy for financial literacy. Individuals who have low financial literacy are less likely to invest in stocks (Van Rooij, Lusardi, and Alessie 2011). Faig and Shum (2004) find the decision to hold stocks is positively correlated with age, labor income, and financial net worth when analyzing the 1992–2001 Survey of Consumer Finances.
Methodology
Three different empirical models are developed in order to analyze the amount of variation in portfolio allocation scores that can be explained by each of the three risk tolerance measures. These models help us understand how well different measures capture the portfolio allocation preference of clients. An additional three models are used to analyze the amount of variation in recent investment changes that can be explained by each of the three measures. These models are important because they help determine which measures best capture actual client behavior. Four models with different combinations of risk tolerance questions are also developed in order to understand the value of including additional measures in a questionnaire.
Three separate ordinal logistic regressions are run, each containing a different risk tolerance measure, with portfolio allocation score as the dependent variable. Three additional ordinal logistic regressions are run with recent investment changes as the dependent variable. Ordinal logistic regression is used because portfolio allocation score and recent investment changes are discrete variables and can be ranked. Three separate ordinary least squares (OLS) regressions are also run with portfolio allocation score as the dependent variable to aid in the interpretability of the results. The coefficient of determination, or r-squared statistic, is the proportion of variation in the dependent variable that can be explained by the independent variables in the model. For this paper it helps us determine how much variability of a client’s portfolio allocation score (or recent investment changes) can be explained by different risk tolerance measures. Because we are comparing regression models with different numbers of independent variables, adjusted r-squared is used in the analysis. The adjusted r-squared statistic takes into account the number of independent variables in the model. Adding an independent variable to a multiple regression model almost always increases the r-squared statistic, even if the variable is not very meaningful. The adjusted r-squared statistic only increases if the additional variable improves the model more than would be expected by chance alone. The pseudo r-squared statistic is used for logistic regression and is a close approximation to the r-squared statistic.
Results
Table 3 shows the differences in adjusted r-squared statistics with portfolio allocation score as the dependent variable. A model containing just the demographic and socioeconomic control variables has an adjusted r-squared statistic of 0.1129 (not reported). This means the proportion of variation in portfolio allocation score that can be explained solely by these variables is 0.1129. When the Arrow-Pratt measure is included in the model the adjusted r-squared statistic is 0.1550. This means the Arrow-Pratt measure explains approximately 37 percent more variation in portfolio allocation score compared with the set of basic demographic and socioeconomic characteristics. The adjusted r-squared statistic for the loss aversion measure is 0.2824. The loss aversion measure explains approximately 82 percent more variation in portfolio allocation score compared with the model with the Arrow-Pratt measure. The model with the self-assessment measure has an adjusted r-squared of 0.3297 and explains approximately 17 percent more variation in portfolio allocation score compared with the model with the loss aversion measure. The model with the self-assessment measure explains approximately 113 percent more variation in portfolio allocation score compared with the model with the Arrow-Pratt measure.
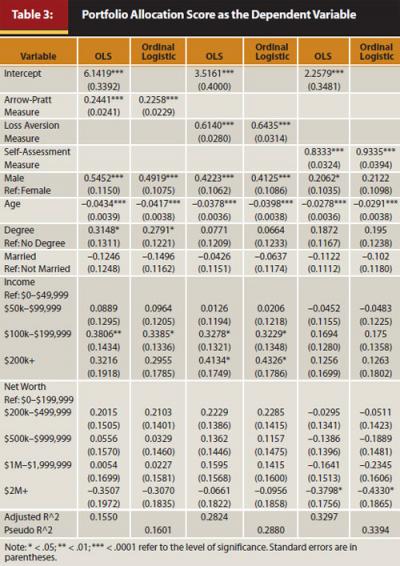
Table 4 examines the extent to which the different risk tolerance measures explain variation in recent investment changes. The pseudo r-squared statistic for the model with the loss aversion measure is 0.1773. The loss aversion model explains approximately 47 percent more variation in recent investment changes compared with the model with the Arrow-Pratt measure. The model with the loss aversion measure explains approximately 7 percent more variation in recent investment changes compared with the model with the self-assessment measure. The model with the self-assessment measure explains approximately 38 percent more variation in recent investment changes compared with the model with the Arrow-Pratt measure.

We also analyze the usefulness of including different measures within a questionnaire with portfolio allocation score as the dependent variable. The model with the loss aversion measure, self-assessment measure, and control variables has an adjusted r-squared of 0.3957. When all three measures are included, the adjusted r-squared statistic is 0.3978. Therefore, when the loss aversion and self-assessment questions are included, adding the Arrow-Pratt questions only explains 0.53 percent more variation in portfolio allocation score.
A similar regression is run that includes different risk tolerance measures within a questionnaire with recent investment changes as the dependent variable. The model with the loss aversion measure, self-assessment measure, and control variables has a pseudo r-squared statistic of .2088. When all three measures and the control variables are included in the model the pseudo r-squared statistic is .2144. Therefore, when the loss aversion and self-assessment questions are included, adding the Arrow-Pratt questions only explains 2.68 percent more variation in recent investment changes.
Conclusions
The results of this study provide planners an empirically tested justification for the inclusion of questions within risk tolerance surveys. Findings from behavioral finance literature would suggest that questions based on loss aversion should be used when determining a client’s portfolio allocation preference. The results of this study help to strengthen this claim. Asking clients simple, straightforward questions regarding the degree of risk they have taken with their financial decisions is also very useful when constructing a risk tolerance questionnaire. Although the Arrow-Pratt measure should theoretically be the best measure of a client’s preference for risky assets, our results indicate that it does not add much value when both loss aversion and self-assessment questions are included in a risk tolerance survey. The appendix provides planners risk tolerance questions based on loss aversion and self-assessment.
These findings are also consistent when testing the measures against recent investment changes made by individuals. This should be especially relevant to planners given that recent investment changes likely encompass changes made during the global financial crisis. It is in times such as these that the assessment of how clients will react to a severe market downturn will be critical in determining whether they continue to follow their planner’s recommendations. If a risk tolerance questionnaire fails to accurately measure a client’s portfolio allocation preference, it is more likely that client will want to shift his or her portfolio to cash during market downturns. This could result in goals being delayed and may ultimately lead to the termination of the adviser.
Although risk tolerance is theoretically assessed in order to estimate the optimal mix of risky and risk-free assets according to modern portfolio theory, there is strong evidence that proper assessment of loss aversion is essential to assessing whether clients are capable of maintaining their risky asset allocations following a decline in equity prices. Individual investors lose on average 1.6 percent annually in dollar-weighted returns because they tend to pull money out of risky mutual funds following a significant decline when equity valuations are most favorable, and conversely increase equity allocation following a recent price increase when valuations are less favorable (Friesen and Sapp 2007). Appropriate client portfolio allocation may involve choosing investments that are both less risky than theoretically optimal, but more likely to provide better long-run performance by increasing the probability the clients will maintain their asset allocations during a recession. This is a topic we hope will be explored in future research.
References
AARP and American Council of Life Insurers (ACLI). 2007. “What Now? How Retirees Manage Money to Make It Last Through Retirement.” http://assets.aarp.org/rgcenter/econ/guaranteed_income.pdf.
Alan, Sule. 2006. “Entry Costs and Stock Market Participation over the Life Cycle.” Review of Economic Dynamics 9, 4: 588–611.
Arrow, Kenneth. 1965. “The Theory of Risk Aversion.” In Aspects of the Theory of Risk-Bearing. Helsinki: Yrjo Jahnssonin Saatio.
Batjelsmit, Vickie L., and Jack A. VanDerhei. 1997. “Risk Aversion and Retirement Income Adequacy.” In Positioning Pensions for the Twenty-First Century. M. S. Gordon, O. S. Mitchell, and M. M. Twinney, eds. Philadelphia: University of Pennsylvania Press. 45–66.
Barsky, Robert B., F. Thomas Juster, Miles S. Kimball, and Matthew D. Shapiro. 1997. “Preference Parameters and Behavioral Heterogeneity: An Experimental Approach in the Health and Retirement Study.” Quarterly Journal of Economics 11, 2: 537–79.
Benartzi, Shlomo, and Richard H. Thaler. 1995. “Myopic Loss Aversion and the Equity Premium Puzzle.” Quarterly Journal of Economics 110, 1: 73–92.
Boyle, Patricia, Lei Yu, Aron Buchman, David Laibson, and David Bennett. 2011. “Cognitive Function Is Associated with Risk Aversion in Community-Based Older Persons.” BMC Geriatrics 11, 53.
Callan, V. J., and M. Johnson. 2003. “Some Guidelines for Financial Planners in Measuring and Advising Clients About Their Levels of Risk Tolerance.” Journal of Personal Finance 1: 31–44.
Campbell, John Y., and N. Gregory Mankiw. 1989. “Consumption, Income, and Interest Rates: Reinterpreting the Time Series Evidence.” NBER Macroeconomics Annual: 185–215.
Christiansen, Charlotte, Jesper Rangvid, and Juanna S. Joensen. 2010. “The Effects of Marriage and Divorce on Financial Investments: Learning to Love or Hate Risk?” http://ssrn.com/abstract=1670612.
Dimmock, Stephen G., and Roy Kouwenberg. 2010. “Loss-Aversion and Household Portfolio Choice.” Journal of Empirical Finance 17, 3: 441–459.
Faig, Miquel, and Pauline Shum. 2006. “What Explains Household Stock Holdings?” Journal of Banking and Finance 30, 9: 2579–2597.
Federal Reserve Board. Survey of Consumer Finances. www.federalreserve.gov/econresdata/scf/scfindex.htm.
Finke, Michael, John Howe, and Sandra Huston. 2011. “Old Age and the Decline in Financial Literacy.” http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1948627.
Friesen, Geoff, and Travis Sapp. 2007. “Mutual Fund Flows and Investor Returns: An Empirical Examination of Fund Investor Timing Ability.” Journal of Banking and Finance 31: 2796–2816.
Grable, John E., and Ruth H. Lytton. 1999. “Financial Risk Tolerance Revisited: The Development of a Risk Assessment Instrument.” Financial Services Review 8: 163–181.
Grable, John E., and Ruth H. Lytton. 2003. “The Development of a Risk Assessment Instrument: A Follow-Up Study.” Financial Services Review 12: 257–274.
Hanna, Sherman D., Jessie X. Fan, and Y. Regina Chang. 1995. “Optimal Life Cycle Savings.” Financial Counseling and Planning 6: 1–15.
Hanna, Sherman D., and Suzanne Lindamood. 2004. “An Improved Measure of Risk Aversion.” Financial Counseling and Planning 15, 2: 27–38.
Hanna, Sherman D., and Suzanne Lindamood. 2010. “Risk Tolerance: Cause or Effect.” Academy of Financial Services. www.academyfinancial.org/09Conference/09Proceedings/(1C)%20Hanna,%20Lindamood.pdf.
Hanna, Sherman. D., William Waller, and Michael Finke. 2008. “The Concept of Risk Tolerance in Personal Financial Planning.” Journal of Personal Finance 7, 1: 96–108.
Hallahan, Terrence A., Robert W. Faff, and Michael D. McKenzie. 2004. “An Empirical Investigation of Personal Financial Risk Tolerance.” Financial Services Review 13: 57–78.
Kasten, Gregory W., and Michael W. Kasten. 2011. “The Impact of Aging on Retirement Income Decision Making.” Journal of Financial Planning (June).
Kahneman, Daniel, and Amos Tversky. 1979. “Prospect Theory: An Analysis of Decision Under Risk.” Econometrica 47: 263–291.
Kahneman, Daniel, and Dan Lovallo. 1993. “Timid Choices and Bold Forecasts: A Cognitive Perspective on Risk Taking.” Management Science 39: 17–31.
Markowitz, Harry. 1952. “Portfolio Selection.” Journal of Finance 7, 1: 77–91.
Modigliani, Franco, and Richard H. Brumberg. 1954. “Utility Analysis and the Consumption Function: An Interpretation of Cross-Section Data.” In Post-Keynesian Economics. Kenneth K. Kurihara, ed. New Brunswick, NJ: Rutgers University Press. 388–436.
Pratt, J. W. 1964. “Risk Aversion in the Small and in the Large.” Econometrica 32 (January–April): 122–136.
Rabin, Matthew. 2000a. “Diminishing Marginal Utility of Wealth Cannot Explain Risk Aversion.” In Choices, Values, and Frames. Daniel Kahneman and Amos Tversky, eds. New York: Cambridge University Press. 202–208.
Rabin, Matthew. 2000b. “Risk Aversion and Expected-Utility Theory: A Calibration Theorem.” Econometrica 68, 5: 1281–1292.
Rabin, Matthew, and Richard H. Thaler. 2001. “Anomalies: Risk Aversion.” Journal of Economic Perspectives 15, 1: 219–232.
Roszkowski, Michael, and John E. Grable. 2005. “Estimating Risk Tolerance: The Degree of Accuracy and the Paramorphic Representations of the Estimate.” Financial Counseling and Planning 16, 2: 29–47.
Roszkowski, Michael J., and Geoff Davey. 2010. “Risk Perception and Risk Tolerance Changes Attributable to the 2008 Economic Crisis: A Subtle but Critical Difference.” Journal of Financial Service Professionals 64: 42–53.
Roszkowski, Michael J., Geoff Davey, and John E. Grable. 2005. “Questioning the Questionnaire Method: Insights on Measuring Risk Tolerance from Psychology and Psychometrics.” Journal of Financial Planning 18, 4: 68–76.
Sahm, Claudia. 2007. “How Much Does Risk Tolerance Change?” Finance and Economics Discussion Series, Division of Research & Statistics and Monetary Affairs, Federal Reserve Board. www.federalreserve.gov/Pubs/Feds/2007/200766/revision/200766pap.pdf.
Sharpe, William. 1964. “Capital Asset Prices: A Theory of Market Equilibrium Under Conditions of Risk.” Journal of Finance 19, 3: 425–442.
Sunden, Annika E., and Brian J. Surette. 1998. “Gender Differences in the Allocation of Assets in Retirement Savings Plans.” American Economic Review, Papers and Proceedings 88: 207–211.
Thaler, Richard H., Amos Tversky, Daniel Kahneman, and Alan Schwartz. 1997. “The Effect of Myopia and Loss Aversion on Risk-Taking: An Experimental Test.” Quarterly Journal of Economics 112: 647−661.
Tversky, Amos, and Daniel Kahneman. 1992. “Advances in Prospect Theory—Cumulative Representation of Uncertainty.” Journal of Risk and Uncertainty 5: 297–323.
Van Rooij, Maarten, Annamaria Lusardi, and Rob Alessie. 2007. “Financial Literacy and Stock Market Participation.” National Bureau of Economic Research Working Paper 13565.
Wang, Kevin Q. 2011. “Buy High and Sell Low.” The China Center for Financial Research, Tsinghua University. www.ccfr.org.cn/cicf2011/papers/20110109125416.pdf.
Winchester, Danielle, Sandra Huston, and Michael Finke. 2011. “Investor Prudence and the Role of Financial Advice.” Journal of Financial Service Professionals 65, 4: 43–51.
Yao, Rui., Sherman Hanna, and Suzanne Lindamood. 2004. “Changes in Financial Risk Tolerance.” Financial Services Review 13, 4: 249–266.
Yook, Ken C., and Robert Everett. 2003. “Assessing Risk Tolerance: Questioning the Questionnaire Method.” Journal of Financial Planning 18, 8: 48–55.
Zeldes, Stephen P. 1989. “Optimal Consumption with Stochastic Income: Deviations from Certainty Equivalence.” Quarterly Journal of Economics 104: 275–298.
Acknowledgments: The authors would like to thank Geoff Davey and FinaMetrica for their contributions to the advancement of risk tolerance research.
