Journal of Financial Planning: May 2011
Jack Brown, CFA, is founder and president of Laureola Asset Management in Naples, Florida.
Travis L. Jones, Ph.D., is associate professor of finance at Florida Gulf Coast University in Fort Myers, Florida, and senior investment strategy adviser at Laureola Asset Management.
Executive Summary
- Asset-liability management (ALM) provides a risk-management technique that focuses on both sides of an investor’s balance sheet, in contrast to traditional asset allocation approaches, which tend to only emphasize investor assets.
- This article presents an application of ALM for financial planners, along the lines of Jones and Brown (2009), using an example of an individual investor who is seeking an asset allocation to best meet future spending needs.
- This ALM methodology determines the fixed-income exposure required to fully or partially immunize an investor’s liabilities, thereby reducing the volatility of the assets required to fund the investor’s liabilities and the shortfall funding risk of the portfolio.
- The result takes into account investor circumstances and market conditions in order to allow a financial planner to better fit an asset allocation to the needs of the investor.
- The goal of this article is to demonstrate this approach and allow financial planners to use ALM in conjunction with existing asset-allocation practices.
The need for financial planners to provide meaningful advice that reflects both the assets and liabilities of an investor’s balance sheet appears to be growing. A recent study by the Employee Benefit Research Institute (EBRI) states that “dramatically high percentages of Americans—even in the upper-income categories—are likely to run short of money after 10 or 20 years of retirement” (EBRI 2010). The EBRI study highlights a balance-sheet deficit faced by many investors. Employing asset-liability management (ALM) would be beneficial, as financial planners seek to balance the risks of investors running out of money with maximizing risk-adjusted portfolio returns.
In this article, we provide some background on ALM research (particularly related to private wealth), discuss some key considerations for financial planners who are considering ALM, and present a practical version of ALM for private clients, along the lines of Jones and Brown (2009). The illustrated example is based on an individual investor who is seeking an asset allocation to best meet future spending needs. The goal of this article is to demonstrate this approach to show financial planners how to use ALM in conjunction with existing asset-allocation practices.
Literature Review
The ALM area of finance has been widely studied for its use in pension funds, insurance companies, and other institutional investment portfolios (see Leibowitz and Henriksson 1988; Waring 2004a, 2004b; Fong and Guin 2007, among others). ALM has only recently begun to be examined in the context of individual investors. Numerous studies examine portfolio management of individual investors within an ALM framework. Stout (2008) presents a stochastic, Monte Carlo optimization of retirement portfolios that seeks to minimize the probability of exhausting the portfolio. He notes that the risk-minimizing allocation to equities decreases with retirement age and increases with the withdrawal rate from the portfolio. Ziemba (2003) presents an ALM methodology for managing multi-period investment horizons using a generalized stochastic program. In his article, individuals’ multi-period horizons are examined against a model that suggests an allocation for each horizon. Further, the EDHEC Risk and Asset Management Research Centre has published a number of general studies dealing with the topic of ALM for individual investors (for example, Amenc, Martellini, and Ziemann 2007).
The application of ALM for individual investors is also examined from a behavioral perspective in various studies. In these studies, liabilities are framed in terms of goals that investors wish to achieve using portfolio funds. Nevins (2004) examines goals-based investing using investor-specific liability goals and sub-portfolios (within the larger investment portfolio) that are managed to meet these goals. Chhabra (2005) also incorporates investor goals into the asset allocation decision and notes that risk allocation should precede asset allocation when managing portfolios for individual investors. Brunel (2006) examines goals-based investment techniques and compares the efficiency of these techniques to traditional allocation approaches; he discovers that the additional costs associated with goals-based investing are trivial.
Jones and Brown (2009) contend that private-wealth investors are challenged in two ways: (1) asset allocation advice yielded from commonly applied techniques focuses on optimization, not risk management, and (2) shortfall funding risk analysis is not typically analyzed in terms of multi-period stochastic reality. They further contend that shortfall risk analysis does not typically provide asset-allocation advice. Their study argues that straightforward and readily implementable risk-management techniques that provide insight on asset allocation are in short supply for private wealth practitioners. Jones and Brown (2009) also contend that the absence of ALM in the private wealth arena stems from two factors: (1) its perceived complexity, and (2) prior attempts to implement ALM across larger firms tended to fail because of the actual complexity of the specific implementation techniques and the associated software, among other reasons. As a result, they present a straightforward interest rate immunization technique in which low-risk assets can ultimately be used to immunize liabilities over a specified period. Further, the net present value of liabilities over the specified immunization horizon is used as a constraint within a mean-variance optimization (MVO). This approach allows an individual’s portfolio to provide short-term cash flow, as needed, while also considering the longer-term demands on the portfolio. Another interpretation of this approach is as a form of liability-driven investing with surplus optimization (Taylor and Earney 2008), which itself falls within the ALM arena.
Ultimately, ALM protects against shortfall funding risks and provides perspective on the basic mix of low-risk (immunizing) assets and riskier assets, whereas widely used asset-allocation techniques such as mean-variance optimization (MVO) focus primarily on optimizing assets. In this regard, the Jones and Brown (2009) approach allows for both liability risk managment and efficient portfolio construction.
Key Considerations of ALM for Financial Planners
The immunization period chosen will affect exhaustion rates. For example, consider an investor with discounted liabilities roughly in line with his investment portfolio. If this investor chooses to fully immunize his liabilities, then a high priority is placed on spending needs and portfolio exhaustion is a greater risk over the long-term. A shorter immunization period, while taking on more portfolio volatility risk, reduces the risk of portfolio exhaustion.
Further, consider a market scenario in which a financial planner has a high level of conviction that interest rates will rise (bond prices fall) and equity markets appreciate. The cost of locking in a fully or near-fully hedged ALM framework would be less than optimal, as alpha-generating securities are projected to increase in value while the present values of liabilities are projected to decrease in value (with higher discounting rates).
There are many factors that would lead to diverging values among assets and liabilities. Liabilities are theoretical in nature, and the present value of the liabilities changes because of modeling factors primarily based on changing discount rates. On the other hand, asset values change based on the actual performance of immunizing assets. Cash-flow matching is largely viewed as the most time-consuming but tightest way to manage asset and liability changes (see Fong and Guin 2007, Waring 2004a). The durations of the liabilities as well as the assets will affect the interest-rate sensitivity of the portfolio. For example, consider a 1 percent increase in rates (assuming a parallel shift in the curve). If assets and liabilities both have durations of seven years, then a 1 percent increase in rates would lead to a 7 percent decrease in both assets and liabilities. On the other hand, if the assets had a duration of 12 years, asset values would fall by 12 percent, while the liabilities fall by 7 percent (see Waring 2004a; Zheng et al. undated for further discussion of how the durations of both assets and liabilities affect the overall interest rate sensitivity of the portfolio).
Partial Immunization
Consequently, while full implementation of an ALM framework might be unreasonable in some circumstances, a moderate move toward an ALM framework would be a step in the right direction. Therefore, a partial or phased-in immunization would make sense for many investors. The example discussed below reflects the initial implementation of a partial immunization for an investor in a deficit balance-sheet position and demonstrates that while a partial immunization may be favorable, a full immunization is not feasible due to a lack of assets required to fully fund expected liabilities.
Balancing the goals of ALM with the challenges of implementation, therefore, means the degree of immunization rests largely on striking a balance between (1) the value of assets versus liabilities, (2) the degree of immunization desired by the client in light of overall investment goals, and (3) market factors. A longer-term goal of increasing the degree of immunization, or even full immunization, rests on the notion that these issues are monitored and acted on over time. On the other hand, investors who have a considerable surplus of assets versus liabilities could implement a fully hedged ALM portfolio for a rather low cost (in terms of immunizing assets as a percentage of total assets).
In actual terms, final portfolio values will be affected by capital market returns and spending. In a very general sense, however, a portfolio with an expected return (based on estimated capital returns by the asset allocation) that exceeds the real return required to maintain wealth is expected to grow in real t
Another consideration of ALM relates to the additional level of work and interaction with clients. Fully understanding, and hence immunizing, the liabilities of an investor requires a deep probing of client circumstances and a degree of actuarial assumptions that may or may not be relevant depending on the investor. For the purpose of this paper, we consider only the assumptions of expected spending and assumed rates of inflation. Myriad assumptions affect modeling liabilities, such as life expectancy, taxes, and changing health-care expenses—some of which depend on the investor and some that may be affected by legislation. Further, the example below might be interpreted as a deterministic view of liabilities, whereas actual liabilities tend to be stochastic in nature based on changing costs, tax considerations, one-time expenses, etc. Consequently, alternative approaches to modeling liabilities that use various probabilistic computational methods, for example, could be employed. As is the challenge with providing advice to investors on a broad level, other considerations that affect ALM relate to actual asset returns deviating from expectations, actual inflation rates deviating from estimates used in modeling liabilities, and changing investor circumstances (such as time horizons or stochastic liabilities).
Consider that this article focuses on identifying the size and duration of an immunizing allocation. For implementation purposes, we propose a broad allocation to investment-grade fixed income that reflects these factors. Also note that immunized portfolios have to be monitored and adjusted periodically to ensure that the liabilities remain immunized as asset values change. Other approaches to immunization include, but are not limited to, the use of interest-rate options, cash-flow matching, and other forms of duration matching.
This article focuses on the computation of assets based on investment portfolio assets and the computation of liabilities based on those directly affecting the investment portfolio. A natural extension of ALM might consider the assets and liabilities of other balance-sheet items such as real estate, family-owned businesses, art collections, and potential legal liabilities, to name a few.
This approach to ALM can be used effectively in conjunction with other traditional asset-allocation techniques such as mean-variance optimization (MVO), Monte Carlo simulation (MCS), surplus optimization, goals-based investing, or most any traditional approach. It would be prudent for practitioners who embrace MVO, for example, to use the results from ALM as an added constraint within an MVO model. For example, ALM might yield an immunization requirement of 50 percent fixed income with a seven-year duration. Hence, a minimum allocation of 50 percent investment-grade fixed income with a seven-year duration could be used as an MVO constraint. As a result, MVO and other asset-allocation techniques tend to complement ALM, helping to improve overall portfolio efficiency and total return. Thus, the financial planner can integrate this approach to ALM into his or her preferred asset-allocation methodology.
With the aforementioned constraints in mind, the example below captures the primary risks associated with shortfall funding and balance-sheet volatility. Further, the approach yields a pragmatic, effective, and readily implementable way to immunize liability risks while allowing for real wealth enhancement.
Process Overview
An investor’s future spending, cash outflows, and capital requirements (the liabilities) are modeled over the lifetime of an investor. Present values of these liabilities are then derived along a suitable market-based yield curve (such as the AA-corporate yield curve). The net present value corresponding to the horizon represents an investor’s total liabilities. Incrementally summed present values for each year in the horizon represent the nominal allocation to low-risk, immunizing assets for a chosen immunization period (in the case of a partially hedged approach). The weighted-average timing of present-value cash flows represents the duration (or interest-rate sensitivity) of liabilities. Duration is measured both for total liabilities and for liabilities of a chosen immunization period. After the degree of immunization is established, a determination can be made regarding the basic allocation to low-risk immunizing assets (high-quality fixed income), and this information can be used as a constraint in the optimization process.
The primary goal of ALM is to reduce shortfall funding risks and allow assets in the portfolio to fund future liabilities. Hence, the degree of immunization implies the degree these risks are reduced. In this light, a trade-off often exists between the level of immunization and alpha potential. Making this determination is dependent on an investor’s level of wealth (assets versus liabilities), his or her goals, and his or her feelings regarding risks associated with future spending and market conditions. Because of these factors, the degree of immunization is determined on a situational basis. In subsequent rebalancing periods, the practitioner should look for opportunities to extend the ALM period as the value of assets versus liabilities improves and as market and client circumstances warrant it.
The next two sections provide the framework and approach to ALM using a simplified but reasonable example. In reality, an investor may have a much more complicated set of circumstances and a financial planner may have a more complex view of market conditions.
Framework of Example
John Doe has $1,000,000 in investable assets and a yearly spending need of $50,000 (see Table 1). This annual spending need will be met by withdrawing funds from the investment portfolio, and the amount will likely change with inflation or other unforeseen lifestyle changes. This withdrawal implies an initial spending rate of 5.0 percent. John is 65 years old with no medical problems and has an investment horizon of 30 years. The risk of assuming a shorter horizon relates to outliving his wealth. He has experienced a decline in portfolio assets as a result of recent investment performance. In response, he has made portfolio adjustments that reflect a lower level of investment risk (reducing overall stock exposure by 10–15 percent). Today, lingering feelings of a dangerous investment environment have led John to emphasize caution.
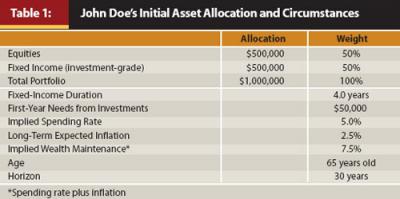
John’s primary goal is having an investment portfolio that supports inflation-adjusted spending needs over time, with a secondary goal of wealth maximization over the investment horizon. Both John and his financial planner believe that interest rates will rise sometime over the next five years or so.
Table 1 shows John’s current asset allocation, which includes a 50 percent allocation to equities and a 50 percent allocation to fixed income (with a duration of four years). As noted in Table 1, long-term inflation is expected to be 2.5 percent per annum. In order to maintain inflation-adjusted wealth, an investment return would have to be approximately 7.5 percent, which includes the spending rate plus inflation.
Asset-Liability Management (ALM)
To determine the basic asset allocation between low-risk (immunizing) and riskier assets, we first identify John Doe’s liabilities over his entire horizon. For modeling liabilities, we apply discount rates (using the AA-rated corporate bond yield curve) to determine the present value of future portfolio outflows. International Accounting Standard 19 notes that the AA-rated corporate bond curve gives appropriate discount rates for pension liabilities; this rate is used here but is only a suggestion for practitioners. In Table 2, the first two columns represent each year in the horizon. Columns 3, 4, and 5 represent the future value of spending (portfolio outflows), the discount rate, and the present value for each yearly cash flow, while the sixth column illustrates the sum of the present value of spending or the dollar allocation required for each level of immunization given the number of years in the future. The final two columns present the percentage of the portfolio allocation required in immunizing assets and the aggregate duration required to immunize those liabilities for the respective periods in the future.
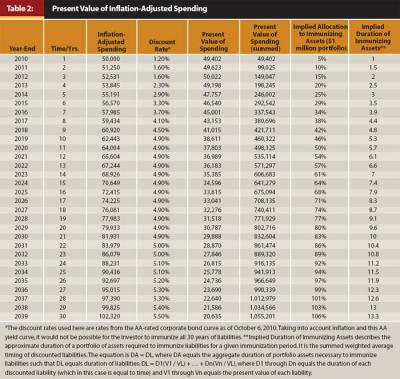
If desired, Treasury Inflation Protected Securities (TIPS) could be used for a portion or all of the future spending offsets. TIPS offer insurance against unforeseen increases in inflation, albeit at a lower yield. For an analysis of using TIPS to secure income needs see Shankar (2009). To incorporate TIPS, adjustments to future values may be required, whereas real yields should be used for discount rates, which are yields on TIPS, for the relative offsetting periods.1
For John Doe, the net present value of liabilities over his entire horizon is $1,055,201, and his portfolio value is $1,000,000. John has a balance-sheet deficit of $55,201; therefore a full hedge against liabilities is not possible with existing portfolio assets—the portfolio would be exhausted—thus this is not considered.
To determine the degree of immunization for John, we consider three scenarios: (1) the current allocation, (2) a partial immunization hedge covering 16 years of liabilities (the proposed solution), and (3) a partial immunization hedge of 25 years. See Table 3.
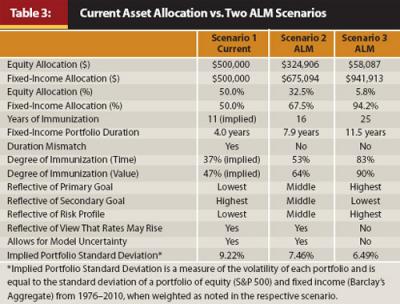
Scenario 1. John Doe has a current (pre-existing) investment-grade fixed-income allocation of $500,000. This represents approximately 11 years’ worth of assets that could be considered as immunizing liabilities (see Table 2). However, the current allocation also presents a duration mismatch of approximately 1.7 years (current duration of 4.0 years versus 5.7 years at year 11 in Table 2). This represents an excess level of changes in assets versus liabilities due to interest rates. With a 50 percent allocation to equities, John has a significant degree of alpha exposure, which would be consistent with his secondary goal of wealth maximization. However, given John’s feelings about risk, we believe it is appropriate to place higher emphasis on his primary goal.
Scenario 2. Scenario 2 reflects our preferred immunization of 16 years (our proposed satisfactory solution) given John’s attitude toward risk, his primary goal of maintaining real retirement income, his secondary goal of wealth maximization, the low interest rate environment, and the overall deficit (total discounted liabilities exceed the investor’s portfolio value). This is a subjective period of immunization that represents a relatively low level of overall portfolio volatility; however, with an overall mix of assets that approximates the wealth maintenance return of 7.5 percent. A case could be made for 15 years or 17 years—the exact period of immunization is up to the financial planner in consultation with the client. A 16-year period, in this example, requires a 67.5 percent allocation ($675,094) to immunizing securities with a duration of 7.9 years. This scenario significantly reduces shortfall funding risk and helps secure future spending needs by increasing the fixed-income allocation by approximately 17.5 percent of portfolio assets and by extending the fixed-income duration from 4.0 years to 7.9 years. Immunizing 16 years’ worth of liabilities represents more than one-half of total liabilities in terms of time (16 of 30 years) and 64 percent of total liabilities ($675,094 of $1,055,201) in terms of value. The remaining 37.5 percent allocation to alpha-generating securities, equities in John Doe’s case, provides the opportunity to grow assets and allows time for interest rates to rise, which would allow for allocation to higher-yielding fixed income when rebalancing.
Scenario 3. Lastly, consider a 25-year immunization, an unsatisfactory scenario. Under this scenario, John has immunized 90 percent of portfolio liabilities ($941,913 of $1,055,201) with an 11.5-year duration for immunizing assets. While this scenario places a high focus on John’s primary goal, he has used 94 percent of his portfolio to achieve this immunization. Little room is provided for imperfections in the modeling process such as unexpected changes in inflation, changes in the horizon period, or surprises in John’s spending. Further, practically no adherence to John’s secondary goal exists, as a 6 percent allocation to equities provides little availability for real wealth enhancement. Ultimately, while this scenario goes the furthest to immunize shortfall funding risks, it would be too expensive in terms of im
Perhaps it is most important to note that the degree of immunization is ultimately subjective, and as such, our alternative scenarios could be represented with different immunization periods. Determining a more precise degree of immunization could be achieved through various approaches. For example, a practitioner could compare implied allocations of various immunization scenarios with expected returns on an efficient frontier, such that the expected return exceeds the internal rate of return required to satisfy liabilities and approximates or exceeds the wealth maintenance return.
After a determination is made as to the degree of immunization, other asset-allocation methods, such as MVO or MCS, could be employed. These asset-allocation approaches would enhance efficiency by helping to direct assets among sub-asset classes or styles. In John Doe’s case, where we favor a partial immunization of 16 years, MVO would employ a minimum allocation of 67.5 percent to investment-grade fixed income with a duration of 7.9 years as a constraint in the model.
Longer-term rebalancing approaches in subsequent client meetings could focus on extending the immunization beyond the initial period and ultimately over the entire horizon. Subsequent meetings would take into account the client’s changing circumstances, changes in asset and liability values, market conditions, and other considerations as reflected in Table 3. Therefore, the time required to achieve full immunization might be several years. In the example, John’s primary goal could theoretically be achieved once he reaches a balance-sheet surplus of assets over the present value of liabilities. Regardless of a surplus, however, John’s secondary goal implies that significant exposure to alpha-generating securities (at least where real returns are expected to be positive) is warranted throughout his horizon.
Conclusion
Broadly, ALM provides a path to risk management by understanding an investor’s balance sheet in terms of current wealth and future portfolio needs. This article presents a solution to the notable absence of liability risk management in the private investor arena by focusing on how a financial planner could implement a full or partial hedge of assets to liabilities. Rebalancing considerations involve updating the analysis of asset and liability valuations, reviewing the degree of immunization, and re-evaluating client circumstances and market conditions. These factors help determine whether a greater degree of immunization should be pursued. For investors who are fully immunized, rebalancing focuses on maintaining a robust relationship between assets and liabilities with further emphasis on enhancing surplus wealth. This approach to ALM allows a financial planner to integrate ALM into his or her preferred asset-allocation methodology.
This article is one of numerous studies supporting the use of ALM within individual investor portfolios. Taking into account the liabilities of individual investors is becoming a greater part of the asset-allocation decision, especially in light of recent market volatility and broad concerns related to retirement income shortfalls. This area of investment analysis is growing, and more studies on this topic are expected to be conducted in the near future.
Endnote
- Depending on the prevailing TIPS yield curve, these securities may not provide sufficient yield to successfully immunize a portfolio. In addition, if real yields increase as other yields (and modeling yields) do not, asset values (TIPS) would decline as liabilities remained stable. In an environment where real yields are arguably set to expand, employing TIPS as a liability hedge would be risky. As always, the practitioner must consider actual yields and maturities before implementing the allocation.
References
Amenc, Noël, Lion
Brunel, J. L. P. 2006. “How Sub-Optimal—If at All—Is Goal-Based Asset Allocation?” Journal of Wealth Management 9, 2: 19–34.
Chhabra, A. B. 2005. “Beyond Markowitz: A Comprehensive Wealth Allocation Framework for Individual Investors.” Journal of Wealth Management 7, 4: 8–34.
EBRI. 2010. “EBRI Retirement Readiness Rating™: What Is Your Rating?” Employee Benefit Research Institute. Accessed October 2010 at www.disabled-world.com/news/seniors/retirement-rating.php.
Fong, H. G., and L. D. Guin. 2007. Fixed-Income Portfolio Management. In Managing Investment Portfolios, eds. J. L. Maginn, D. L. Tuttle, D. W. McLeavey, and J. E. Pinto. Hoboken, NJ: Wiley & Sons Inc.
Jones, T. L., and J. Brown. 2009. “Integrating Asset-Liability Risk Management with Portfolio Optimization for Individual Investors.” Journal of Wealth Management 12, 3: 51–60.
Leibowitz, M. L., and R. D. Henriksson. 1988. “Portfolio Optimization Within a Surplus Framework.” Financial Analyst Journal 44, 2: 43–51.
Nevins, D. 2004. “Goals-Based Investing: Integrating Traditional and Behavioral Finance.” Journal of Wealth Management 6, 4: 8–16.
Shankar, S. G. 2009. “A New Strategy to Guarantee Retirement Income Using TIPS and Longevity Insurance.” Financial Services Review 18, 1: 53–68.
Stout, R. G. 2008. “Stochastic Optimization of Retirement Portfolio Asset Allocations and Withdrawals." Financial Services Review 17, 1:1-15.
Taylor, J., and D. Earney. 2008. “Liability Driven Investments.” Principal Global Investors white paper. Accessed July 2009 at https://secure02.principal.com/allweb/docs/RIS/ff/ff5927a.pdf.
Waring, M. B. 2004a. “Liability-Relative Investing.” The Journal of Portfolio Management 30, 4: 8–20.
Waring, M. B. 2004b. “Liability-Relative Investing II.” The Journal of Portfolio Management 31, 1: 40–53.
Zheng, H., L. C. Thomas, and D. E. Allen. (undated). “The Duration Derby: A Comparison of Duration Based Strategies in Asset Liability Management.” White paper available at http://ssrn.com/abstract=266690.
Ziemba, W. 2003. The Stochastic Programming Approach to Asset, Liability, and Wealth Management. Charlottesville, VA: The Research Foundation of CFA Institute.